Keywords
Reynolds stress, shear flow, fieldAverage, variance, covariance
In the simulations of wall-bounded turbulent flows, such as turbulent channel flow [1], the distributions of the Reynolds stress components in the wall-normal direction are matters of interest to researchers and engineers.
For a statistically steady turbulent flow, a prime-squared mean of the velocity field (UPrime2Mean in OpenFOAM) gives the Reynolds stress field
\frac{1}{N} \sum_{k=1}^{N} \left( U_i^{(k)} – \overline{U_i} \right)^2
&=& \frac{1}{N} \sum_{k=1}^{N} {u_{i}^{(k)}}^2 \\
&=& \frac{1}{N} \sum_{k=1}^{N}
\left[
\begin{array}{ccc}
u_{1}^{(k)}u_{1}^{(k)} & u_{1}^{(k)}u_{2}^{(k)} & u_{1}^{(k)}u_{3}^{(k)} \\
u_{2}^{(k)}u_{1}^{(k)} & u_{2}^{(k)}u_{2}^{(k)} & u_{2}^{(k)}u_{3}^{(k)} \\
u_{3}^{(k)}u_{1}^{(k)} & u_{3}^{(k)}u_{2}^{(k)} & u_{3}^{(k)}u_{3}^{(k)}
\end{array}
\right] \\
&=&
\left[
\begin{array}{ccc}
\overline{u_{1}u_{1}} & \overline{u_{1}u_{2}} & \overline{u_{1}u_{3}} \\
\overline{u_{2}u_{1}} & \overline{u_{2}u_{2}} & \overline{u_{2}u_{3}} \tag{1} \\
\overline{u_{3}u_{1}} & \overline{u_{3}u_{2}} & \overline{u_{3}u_{3}}
\end{array}
\right], \\
\end{eqnarray}
where \(U_i^{(k)}\) denotes the instantaneous velocity field \(U_i(\boldsymbol{x}, k\Delta t)\) and it is decomposed into the time-averaged mean \(\overline{U_i}\) and fluctuating components \({u_{i}}^{(k)}\),
\begin{equation}
{U_{i}}^{(k)} = \overline{U_i} + {u_{i}}^{(k)}. \tag{2}
\end{equation}
The diagonal components of the Reynolds stress tensor are the variances of the velocity components and the off-diagonal elements are the covariances of them.
| Function Object – fieldAverage |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
functions { fieldAverage1 { type fieldAverage; libs ("libfieldFunctionObjects.so"); writeControl writeTime; fields ( U { mean on; prime2Mean on; base time; } ); } } |
| Turbulent Channel Flow |
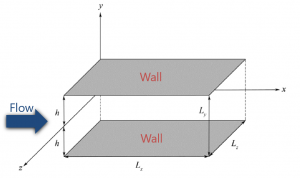
Turbulent channel flow is one of the most fundamental wall-bounded shear flows and it has been widely used to study the structure of near-wall turbulence. Many DNS calculations have been carried out and produced a lot of informative data, which has contributed considerably to the improvements of other turbulence models, such as RANS and LES.
Moser et al. have released the statistical data obtained from their DNS of turbulent channel flow on their web site [2]. The data set contains, among other information, the components of the Reynolds stress tensor at three Reynolds numbers
\begin{equation}
Re_{\tau} = \frac{u_{\tau}h}{\nu} \approx 180,\; 395,\; 590, \tag{3}
\end{equation}
where \(u_{\tau}\) is the friction velocity, \(h\) is the channel half-height and \(\nu\) is the kinematic viscosity.
I will post my DNS results, which will help us to understand the flow behaviors in the near-wall region. The channel395 tutorial in OpenFOAM is the case of large eddy simulation (LES) instead of DNS at \(Re_{\tau}=395\).
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 |
# The data in this file was extracted from a direct numerical # simulation of fully developed plane turbulent channel # flow. Particulars are listed below. Note that some of the statistical # quantities provided in this data set should be zero due to # (statistical) symmetries in the flow. These quantities are reported # here none-the-less as an indicator of the quality of the statistics. # more statistics from this data set are available at # http://www.tam.uiuc.edu/Faculty/Moser/channel # # Authors: Moser, Kim & Mansour # Reference: DNS of Turbulent Channel Flow up to Re_tau=590, 1999, # Physics of Fluids, vol 11, 943-945. # Numerical Method: Kim, Moin & Moser, 1987, J. Fluid Mech. vol 177, 133-166 # Re_tau = 392.24 # Normalization: U_tau, h # Description: Components of the Reynolds stress tensor # Filename: chan395/profiles/chan395.reystress # Date File Created: Mar 01, 2000 # #---End of Header--- # # ny = 257, Re = 392.24 # # y y+ R_uu R_vv R_ww R_uv R_uw R_vw # 0.0000e+00 0.0000e+00 5.3376e-28 4.9018e-29 5.9575e-28 1.1206e-30 -6.1282e-30 6.2793e-32 7.5298e-05 2.9535e-02 1.3684e-04 9.4734e-11 5.2943e-05 -2.4414e-08 5.9464e-08 -2.8525e-11 3.0118e-04 1.1814e-01 2.1828e-03 2.3603e-08 8.2715e-04 -1.5728e-06 8.3228e-07 -1.7141e-09 6.7762e-04 2.6579e-01 1.1020e-02 5.7878e-07 4.0392e-03 -1.8113e-05 3.3616e-06 -1.9051e-08 1.2045e-03 4.7248e-01 3.4718e-02 5.4400e-06 1.2147e-02 -1.0324e-04 1.0732e-05 -1.0411e-07 1.8819e-03 7.3816e-01 8.4454e-02 3.0014e-05 2.7852e-02 -4.0027e-04 2.8297e-05 -3.8272e-07 2.7095e-03 1.0628e+00 1.7438e-01 1.1756e-04 5.3564e-02 -1.2143e-03 6.6865e-05 -1.0969e-06 3.6874e-03 1.4464e+00 3.2123e-01 3.6204e-04 9.0947e-02 -3.1009e-03 1.4506e-04 -2.6288e-06 4.8153e-03 1.8888e+00 5.4336e-01 9.3203e-04 1.4062e-01 -6.9486e-03 2.9097e-04 -5.4596e-06 6.0930e-03 2.3900e+00 8.5851e-01 2.0879e-03 2.0209e-01 -1.4015e-02 5.4723e-04 -1.0091e-05 7.5205e-03 2.9499e+00 1.2802e+00 4.1852e-03 2.7384e-01 -2.5858e-02 9.7373e-04 -1.7119e-05 9.0974e-03 3.5684e+00 1.8132e+00 7.6610e-03 3.5369e-01 -4.4135e-02 1.6529e-03 -2.7764e-05 1.0823e-02 4.2455e+00 2.4490e+00 1.3005e-02 4.3919e-01 -7.0276e-02 2.6847e-03 -4.4587e-05 1.2699e-02 4.9810e+00 3.1644e+00 2.0724e-02 5.2804e-01 -1.0513e-01 4.1721e-03 -7.1044e-05 1.4722e-02 5.7748e+00 3.9229e+00 3.1300e-02 6.1834e-01 -1.4869e-01 6.1889e-03 -1.0893e-04 1.6895e-02 6.6268e+00 4.6811e+00 4.5157e-02 7.0871e-01 -1.9999e-01 8.7562e-03 -1.5460e-04 1.9215e-02 7.5369e+00 5.3953e+00 6.2636e-02 7.9819e-01 -2.5724e-01 1.1834e-02 -1.9552e-04 2.1683e-02 8.5049e+00 6.0286e+00 8.3971e-02 8.8610e-01 -3.1808e-01 1.5387e-02 -2.1029e-04 2.4298e-02 9.5307e+00 6.5558e+00 1.0928e-01 9.7178e-01 -3.8001e-01 1.9449e-02 -1.7262e-04 2.7060e-02 1.0614e+01 6.9642e+00 1.3854e-01 1.0545e+00 -4.4073e-01 2.4133e-02 -6.0490e-05 2.9969e-02 1.1755e+01 7.2524e+00 1.7162e-01 1.1333e+00 -4.9837e-01 2.9501e-02 1.3268e-04 3.3024e-02 1.2953e+01 7.4274e+00 2.0824e-01 1.2075e+00 -5.5162e-01 3.5418e-02 3.9086e-04 3.6224e-02 1.4209e+01 7.5016e+00 2.4803e-01 1.2762e+00 -5.9969e-01 4.1511e-02 6.7818e-04 3.9569e-02 1.5521e+01 7.4897e+00 2.9050e-01 1.3387e+00 -6.4224e-01 4.7330e-02 9.5511e-04 4.3060e-02 1.6890e+01 7.4069e+00 3.3510e-01 1.3948e+00 -6.7924e-01 5.2512e-02 1.1989e-03 4.6694e-02 1.8315e+01 7.2679e+00 3.8121e-01 1.4444e+00 -7.1090e-01 5.6926e-02 1.4016e-03 5.0472e-02 1.9797e+01 7.0865e+00 4.2818e-01 1.4878e+00 -7.3759e-01 6.0659e-02 1.5532e-03 5.4393e-02 2.1335e+01 6.8750e+00 4.7535e-01 1.5251e+00 -7.5980e-01 6.3835e-02 1.6360e-03 5.8456e-02 2.2929e+01 6.6441e+00 5.2211e-01 1.5568e+00 -7.7810e-01 6.6418e-02 1.6465e-03 6.2661e-02 2.4578e+01 6.4025e+00 5.6790e-01 1.5833e+00 -7.9302e-01 6.8207e-02 1.6026e-03 6.7007e-02 2.6283e+01 6.1573e+00 6.1229e-01 1.6047e+00 -8.0503e-01 6.9001e-02 1.5073e-03 7.1494e-02 2.8043e+01 5.9141e+00 6.5493e-01 1.6216e+00 -8.1452e-01 6.8896e-02 1.3268e-03 7.6120e-02 2.9858e+01 5.6767e+00 6.9554e-01 1.6344e+00 -8.2184e-01 6.8285e-02 1.0303e-03 8.0886e-02 3.1727e+01 5.4477e+00 7.3388e-01 1.6439e+00 -8.2733e-01 6.7481e-02 6.4119e-04 8.5790e-02 3.3651e+01 5.2291e+00 7.6971e-01 1.6512e+00 -8.3133e-01 6.6450e-02 2.3642e-04 9.0832e-02 3.5628e+01 5.0223e+00 8.0285e-01 1.6567e+00 -8.3412e-01 6.4937e-02 -1.3612e-04 9.6011e-02 3.7660e+01 4.8279e+00 8.3316e-01 1.6606e+00 -8.3590e-01 6.2875e-02 -4.7569e-04 1.0133e-01 3.9744e+01 4.6462e+00 8.6061e-01 1.6623e+00 -8.3683e-01 6.0710e-02 -7.8412e-04 1.0678e-01 4.1882e+01 4.4768e+00 8.8520e-01 1.6618e+00 -8.3700e-01 5.9182e-02 -1.0539e-03 1.1236e-01 4.4073e+01 4.3194e+00 9.0700e-01 1.6594e+00 -8.3649e-01 5.8527e-02 -1.2655e-03 1.1808e-01 4.6316e+01 4.1730e+00 9.2607e-01 1.6553e+00 -8.3523e-01 5.8437e-02 -1.4126e-03 1.2393e-01 4.8611e+01 4.0370e+00 9.4247e-01 1.6500e+00 -8.3321e-01 5.8512e-02 -1.4930e-03 1.2991e-01 5.0958e+01 3.9106e+00 9.5626e-01 1.6439e+00 -8.3044e-01 5.8376e-02 -1.5118e-03 1.3603e-01 5.3356e+01 3.7930e+00 9.6754e-01 1.6373e+00 -8.2687e-01 5.8084e-02 -1.5196e-03 1.4227e-01 5.5805e+01 3.6834e+00 9.7651e-01 1.6299e+00 -8.2252e-01 5.8125e-02 -1.6228e-03 1.4864e-01 5.8305e+01 3.5821e+00 9.8341e-01 1.6209e+00 -8.1762e-01 5.8537e-02 -1.8295e-03 1.5515e-01 6.0855e+01 3.4896e+00 9.8850e-01 1.6105e+00 -8.1249e-01 5.8809e-02 -2.0145e-03 1.6178e-01 6.3456e+01 3.4053e+00 9.9197e-01 1.5991e+00 -8.0726e-01 5.8494e-02 -2.0826e-03 1.6853e-01 6.6105e+01 3.3278e+00 9.9396e-01 1.5872e+00 -8.0180e-01 5.7876e-02 -2.1101e-03 1.7541e-01 6.8804e+01 3.2557e+00 9.9455e-01 1.5754e+00 -7.9592e-01 5.7034e-02 -2.1628e-03 1.8242e-01 7.1551e+01 3.1886e+00 9.9379e-01 1.5637e+00 -7.8961e-01 5.5746e-02 -2.2441e-03 1.8954e-01 7.4347e+01 3.1269e+00 9.9183e-01 1.5510e+00 -7.8296e-01 5.4259e-02 -2.3220e-03 1.9679e-01 7.7191e+01 3.0702e+00 9.8887e-01 1.5367e+00 -7.7613e-01 5.2957e-02 -2.3519e-03 2.0416e-01 8.0082e+01 3.0178e+00 9.8512e-01 1.5212e+00 -7.6929e-01 5.1819e-02 -2.3018e-03 2.1165e-01 8.3020e+01 2.9678e+00 9.8075e-01 1.5052e+00 -7.6243e-01 5.0872e-02 -2.0851e-03 2.1926e-01 8.6005e+01 2.9191e+00 9.7583e-01 1.4889e+00 -7.5552e-01 5.0514e-02 -1.6209e-03 2.2699e-01 8.9035e+01 2.8712e+00 9.7044e-01 1.4721e+00 -7.4851e-01 5.0564e-02 -8.5802e-04 2.3483e-01 9.2112e+01 2.8239e+00 9.6465e-01 1.4551e+00 -7.4146e-01 5.0229e-02 1.1783e-04 2.4279e-01 9.5234e+01 2.7776e+00 9.5846e-01 1.4379e+00 -7.3445e-01 4.9171e-02 1.0337e-03 2.5086e-01 9.8400e+01 2.7324e+00 9.5179e-01 1.4206e+00 -7.2737e-01 4.7565e-02 1.6440e-03 2.5905e-01 1.0161e+02 2.6883e+00 9.4459e-01 1.4035e+00 -7.2012e-01 4.5716e-02 1.9851e-03 2.6735e-01 1.0486e+02 2.6453e+00 9.3679e-01 1.3867e+00 -7.1271e-01 4.3916e-02 2.2291e-03 2.7575e-01 1.0816e+02 2.6031e+00 9.2845e-01 1.3696e+00 -7.0521e-01 4.2134e-02 2.4143e-03 2.8427e-01 1.1150e+02 2.5612e+00 9.1976e-01 1.3515e+00 -6.9761e-01 4.0077e-02 2.5128e-03 2.9289e-01 1.1489e+02 2.5196e+00 9.1087e-01 1.3322e+00 -6.8985e-01 3.7520e-02 2.5006e-03 3.0162e-01 1.1831e+02 2.4793e+00 9.0185e-01 1.3118e+00 -6.8192e-01 3.4358e-02 2.3726e-03 3.1046e-01 1.2178e+02 2.4411e+00 8.9268e-01 1.2910e+00 -6.7396e-01 3.0858e-02 2.1952e-03 3.1940e-01 1.2528e+02 2.4055e+00 8.8335e-01 1.2700e+00 -6.6598e-01 2.7094e-02 2.0517e-03 3.2844e-01 1.2883e+02 2.3714e+00 8.7385e-01 1.2488e+00 -6.5794e-01 2.3371e-02 1.9999e-03 3.3758e-01 1.3242e+02 2.3380e+00 8.6418e-01 1.2276e+00 -6.4977e-01 2.0500e-02 1.9700e-03 3.4683e-01 1.3604e+02 2.3046e+00 8.5436e-01 1.2066e+00 -6.4148e-01 1.8795e-02 1.8189e-03 3.5617e-01 1.3971e+02 2.2708e+00 8.4439e-01 1.1855e+00 -6.3298e-01 1.7891e-02 1.4336e-03 3.6561e-01 1.4341e+02 2.2365e+00 8.3421e-01 1.1641e+00 -6.2415e-01 1.7572e-02 7.5375e-04 3.7514e-01 1.4715e+02 2.2023e+00 8.2369e-01 1.1423e+00 -6.1500e-01 1.7517e-02 -7.9290e-05 3.8477e-01 1.5092e+02 2.1682e+00 8.1285e-01 1.1202e+00 -6.0551e-01 1.7095e-02 -8.3720e-04 3.9449e-01 1.5474e+02 2.1335e+00 8.0181e-01 1.0983e+00 -5.9561e-01 1.5913e-02 -1.3413e-03 4.0430e-01 1.5858e+02 2.0983e+00 7.9074e-01 1.0767e+00 -5.8530e-01 1.4306e-02 -1.5771e-03 4.1420e-01 1.6247e+02 2.0631e+00 7.7968e-01 1.0551e+00 -5.7460e-01 1.2812e-02 -1.5179e-03 4.2419e-01 1.6639e+02 2.0277e+00 7.6856e-01 1.0339e+00 -5.6350e-01 1.1907e-02 -1.1762e-03 4.3427e-01 1.7034e+02 1.9920e+00 7.5731e-01 1.0131e+00 -5.5204e-01 1.1640e-02 -7.0498e-04 4.4443e-01 1.7433e+02 1.9568e+00 7.4588e-01 9.9279e-01 -5.4040e-01 1.1503e-02 -2.0689e-04 4.5467e-01 1.7834e+02 1.9229e+00 7.3425e-01 9.7254e-01 -5.2883e-01 1.1097e-02 2.0529e-04 4.6500e-01 1.8239e+02 1.8896e+00 7.2249e-01 9.5187e-01 -5.1747e-01 1.0218e-02 5.0971e-04 4.7541e-01 1.8648e+02 1.8562e+00 7.1064e-01 9.3057e-01 -5.0626e-01 9.0004e-03 7.6211e-04 4.8590e-01 1.9059e+02 1.8232e+00 6.9862e-01 9.0936e-01 -4.9507e-01 7.8753e-03 9.2292e-04 4.9646e-01 1.9473e+02 1.7908e+00 6.8642e-01 8.8926e-01 -4.8386e-01 7.1617e-03 9.3017e-04 5.0710e-01 1.9891e+02 1.7591e+00 6.7417e-01 8.7042e-01 -4.7269e-01 7.0121e-03 7.2814e-04 5.1782e-01 2.0311e+02 1.7274e+00 6.6201e-01 8.5243e-01 -4.6164e-01 7.3802e-03 2.7352e-04 5.2860e-01 2.0734e+02 1.6948e+00 6.5007e-01 8.3469e-01 -4.5072e-01 8.2299e-03 -2.9303e-04 5.3946e-01 2.1160e+02 1.6610e+00 6.3843e-01 8.1690e-01 -4.3999e-01 9.3954e-03 -7.4565e-04 5.5039e-01 2.1589e+02 1.6264e+00 6.2712e-01 7.9939e-01 -4.2949e-01 1.0585e-02 -9.5384e-04 5.6138e-01 2.2020e+02 1.5910e+00 6.1613e-01 7.8241e-01 -4.1910e-01 1.1834e-02 -9.5389e-04 5.7244e-01 2.2454e+02 1.5550e+00 6.0545e-01 7.6587e-01 -4.0876e-01 1.3728e-02 -1.0075e-03 5.8357e-01 2.2890e+02 1.5184e+00 5.9512e-01 7.4931e-01 -3.9853e-01 1.6563e-02 -1.2970e-03 5.9476e-01 2.3329e+02 1.4808e+00 5.8523e-01 7.3258e-01 -3.8843e-01 1.9835e-02 -1.7620e-03 6.0601e-01 2.3770e+02 1.4425e+00 5.7589e-01 7.1572e-01 -3.7835e-01 2.2555e-02 -2.2305e-03 6.1732e-01 2.4214e+02 1.4037e+00 5.6715e-01 6.9868e-01 -3.6810e-01 2.3965e-02 -2.5637e-03 6.2868e-01 2.4660e+02 1.3647e+00 5.5896e-01 6.8159e-01 -3.5761e-01 2.4099e-02 -2.7183e-03 6.4010e-01 2.5108e+02 1.3260e+00 5.5120e-01 6.6492e-01 -3.4695e-01 2.3378e-02 -2.7095e-03 6.5158e-01 2.5558e+02 1.2881e+00 5.4372e-01 6.4916e-01 -3.3621e-01 2.2236e-02 -2.5722e-03 6.6311e-01 2.6010e+02 1.2513e+00 5.3642e-01 6.3424e-01 -3.2544e-01 2.0871e-02 -2.4646e-03 6.7469e-01 2.6464e+02 1.2162e+00 5.2919e-01 6.2001e-01 -3.1468e-01 1.9224e-02 -2.5472e-03 6.8632e-01 2.6920e+02 1.1827e+00 5.2197e-01 6.0660e-01 -3.0393e-01 1.7273e-02 -2.7871e-03 6.9799e-01 2.7378e+02 1.1500e+00 5.1473e-01 5.9377e-01 -2.9315e-01 1.5116e-02 -3.0094e-03 7.0972e-01 2.7838e+02 1.1175e+00 5.0750e-01 5.8101e-01 -2.8231e-01 1.3055e-02 -3.1202e-03 7.2148e-01 2.8300e+02 1.0843e+00 5.0029e-01 5.6815e-01 -2.7133e-01 1.1360e-02 -3.1772e-03 7.3329e-01 2.8763e+02 1.0507e+00 4.9312e-01 5.5541e-01 -2.6019e-01 9.9787e-03 -3.2410e-03 7.4513e-01 2.9227e+02 1.0173e+00 4.8605e-01 5.4304e-01 -2.4893e-01 8.7677e-03 -3.3171e-03 7.5702e-01 2.9694e+02 9.8478e-01 4.7922e-01 5.3113e-01 -2.3753e-01 7.8868e-03 -3.3738e-03 7.6894e-01 3.0161e+02 9.5377e-01 4.7268e-01 5.1971e-01 -2.2605e-01 7.6156e-03 -3.4135e-03 7.8090e-01 3.0630e+02 9.2454e-01 4.6644e-01 5.0882e-01 -2.1462e-01 7.9424e-03 -3.4897e-03 7.9289e-01 3.1101e+02 8.9706e-01 4.6047e-01 4.9853e-01 -2.0326e-01 8.6379e-03 -3.6720e-03 8.0491e-01 3.1572e+02 8.7113e-01 4.5478e-01 4.8883e-01 -1.9188e-01 9.5840e-03 -3.9882e-03 8.1696e-01 3.2045e+02 8.4645e-01 4.4932e-01 4.7982e-01 -1.8043e-01 1.0540e-02 -4.3896e-03 8.2904e-01 3.2519e+02 8.2296e-01 4.4410e-01 4.7164e-01 -1.6898e-01 1.1159e-02 -4.7685e-03 8.4114e-01 3.2993e+02 8.0062e-01 4.3915e-01 4.6392e-01 -1.5752e-01 1.1209e-02 -5.0417e-03 8.5327e-01 3.3469e+02 7.7929e-01 4.3458e-01 4.5618e-01 -1.4601e-01 1.0617e-02 -5.1687e-03 8.6542e-01 3.3946e+02 7.5889e-01 4.3044e-01 4.4842e-01 -1.3442e-01 9.5260e-03 -5.1040e-03 8.7759e-01 3.4423e+02 7.3932e-01 4.2671e-01 4.4071e-01 -1.2272e-01 8.2998e-03 -4.8287e-03 8.8978e-01 3.4901e+02 7.2051e-01 4.2339e-01 4.3345e-01 -1.1094e-01 7.2287e-03 -4.4056e-03 9.0198e-01 3.5380e+02 7.0261e-01 4.2046e-01 4.2708e-01 -9.9120e-02 6.4502e-03 -3.8984e-03 9.1420e-01 3.5859e+02 6.8576e-01 4.1796e-01 4.2169e-01 -8.7301e-02 6.1696e-03 -3.3462e-03 9.2644e-01 3.6339e+02 6.7023e-01 4.1591e-01 4.1709e-01 -7.5441e-02 6.4277e-03 -2.7927e-03 9.3868e-01 3.6819e+02 6.5620e-01 4.1431e-01 4.1319e-01 -6.3452e-02 7.0238e-03 -2.2376e-03 9.5093e-01 3.7300e+02 6.4389e-01 4.1313e-01 4.0984e-01 -5.1252e-02 7.7818e-03 -1.6855e-03 9.6319e-01 3.7781e+02 6.3375e-01 4.1234e-01 4.0689e-01 -3.8772e-02 8.7489e-03 -1.1858e-03 9.7546e-01 3.8262e+02 6.2626e-01 4.1188e-01 4.0431e-01 -2.6001e-02 9.8627e-03 -7.6554e-04 9.8773e-01 3.8743e+02 6.2174e-01 4.1166e-01 4.0247e-01 -1.3031e-02 1.0731e-02 -3.8835e-04 1.0000e-00 3.9224e+02 6.2024e-01 4.1160e-01 4.0179e-01 0.0000e+00 1.1032e-02 0.0000e+00 |
| References |
[1] R. D. Moser, J. Kim and N. N. Mansour, Direct numerical simulation of turbulent channel flow up to \({\rm Re}_{\tau}\)=590. Physics of Fluids 11(4), 943-945, 1999.
[2] DNS Data for Turbulent Channel Flow. Available at: http://turbulence.ices.utexas.edu/data/MKM/ [Accessed: 9 April 2017].
[3] turbulence.ices.utexas.edu file server. Available at: http://turbulence.ices.utexas.edu/ [Accessed: 4 May 2017].
great post, Thanks a lot.
This post is very helpful. I also would like to know how do you usually calculate U_rms and u'(turbulence intensity) in OpenFOAM?
Thanks for the informative post. I think it’ll be useful to mention that the Reynolds stresses obtained through the procedure you mention are the resolved stresses for LES, and not the total stresses.