Last Updated: May 4, 2019
Large Eddy Simulation (LES) can be used to accurately simulate unsteady flow behaviors but its numerical cost is higher compared to the conventional Reynolds Averaged Navier-Stokes (RANS) approach.
Several methods have been developed in order to save computational time and cost for unsteady flow computations compared to LES.
Keywords
Detached-Eddy Simulation (DES), Scale Adaptive Simulation (SAS), Grey area problem
Detached Eddy Simulation (DES)
Detached-Eddy Simulation (DES) is a hybrid Reynolds Averaged Navier-Stokes/Large-Eddy Simulation model. The DES model was first proposed in 1997 by Spalart et al. [1] based on the Spalart-Allmaras RANS model and it is commonly referred to as DES97.
Spalart-Allmaras Based DES Formulation (DES97)
Its formulation is briefly described in [2]:
The driving length scale of the RANS S-A model is the distance to the closest wall, \(d\). This makes a modification to this model for DES mode quite straightforward (exactly for this reason it was used as a basis of DES in the first publication [1]). The modification consists in substituting for \(d\), everywhere in the equations, the new DES length scale, \(\tilde{d}\). This length is also based on the grid spacing \(\Delta\) and is defined as:
\begin{equation}
\tilde{d} = {\rm min}\left( d, C_{DES}\Delta \right), \tag{1} \label{eq:dTilda}
\end{equation}
where \(C_{DES}\) is the only new adjustable model constant, and \(\Delta\) is based on the largest dimension of the local grid cell
\begin{equation}
\Delta = {\rm max}\left( \delta_{x}, \delta_{y}, \delta_{z} \right). \tag{2} \label{eq:delta}
\end{equation}
Here we assume for simplicity that the grid is structured and that the coordinates \(\left(x, y, z\right)\) are aligned with the grid cell, but the generalizations are obvious.For wall-bounded separated flows, the above formulation results in a bybrid model that functions as the standard RANS S-A model inside the whole attached boundary layer, and as its subgrid-scale version in the rest of the flow including the separated regions and near wake. Indeed, in the attached boundary layer, due to the significant grid anisotropy \(\left(\delta_{x} \approx \delta_{z} \gg \delta_{y}\right)\) typical of this flow region, in accordance with \eqref{eq:dTilda}, \(\tilde{d} = d\), and the model reduces to the standard S-A RANS model. Otherwise, once a field point is far enough from walls \(\left( d > C_{DES}\Delta \right)\), the length scale of the model becomes grid-dependent, i.e., the model performs as a subgrid-scale version of the S-A model. Note that at “equilibrium” (meaning a balance of production and destruction terms) this model reduces to an algebraic miximg-length Smagorinski-like subgrid model.
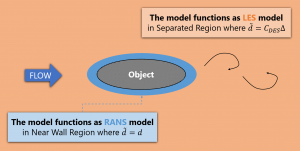
The “DES limiter” defined by Eq. \eqref{eq:dTilda} that is used in DES97 switches between the RANS length scale and LES length scale so that the model behaves in RANS-like and LES-like manners as illustrated in Figure 1. The length scale \eqref{eq:dTilda} depends only on the grid used in the simulation and it is solution-independent.
- Spalart-Allmaras DES model
- Spalart-Allmaras DDES model
- Spalart-Allmaras IDDES model
Menter’s SST Based DES Formulation
- k-\(\omega\) SST DES model
- k-\(\omega\) SST DDES model
- k-\(\omega\) SST IDDES model
There is a project called DESider (Detached Eddy Simulation for Industrial Aerodynamics) and many other DES models have been developed based on different RANS models, including RSM ones.
Other Models
- \(v^2-f\) DES model
We can check the RANS and LES regions using the DESModelRegions function objects in OpenFOAM.
Scale Adaptive Simulation (SAS)
- k-\(\omega\) SST SAS model
Useful Links
- FLOMANIA (Flow Physics Modelling An Integrated Approach) Project: 2002-2004
- DESider (Detached Eddy Simulation for Industrial Aerodynamics) Project: 2004-2007
- ATAAC (Advanced Turbulence Simulation for Aerodynamic Application Challenges) Project
References
[1] P. R. Spalart, W.-H. Jou, M. Strelets and S. R. Allmaras, Comments on the feasibility of LES for wings, and on a hybrid RANS/LES approach. 1st AFOSR Int. Conf. on DNS/LES, Aug. 4-8, 1997, Ruston, LA. In “Advances in DNS/LES”, C. Liu and Z. Liu Eds., Greyden Press, Columbus, OH.
[2] M. Strelets, Detached Eddy Simulation of Massively Separated Flows. AIAA, 2001-0879.
[3] P. R. Spalart, S. Deck, M. L. Shur, K. D. Squires, M. Kh. Strelets, and A. Travin, A new version of detached-eddy simulation, resistant to ambiguous grid densities. Theoretical and Computational Fluid Dynamics, 20(3), 181-195, 2006.
[4] M. L. Shur, P. R. Spalart, M. Kh. Strelets, and A. Travin, A hybrid RANS-LES approach with delayed-DES and wall-modelled LES capabilities. International Journal of Heat and Fluid Flow, 29, 1638–1648, 2008.
[5] Detached eddy simulation (DES). Available at: http://www.cfd-online.com/Wiki/Detached_eddy_simulation_(DES) [Accessed: 03 May 2019].
[6] OpenFOAM® v3.0+: New Solver and Physical Modelling Functionality. Available at: https://www.openfoam.com/releases/openfoam-v3.0+/solvers-and-physics.php#physics-kOmegaSSTDES [Accessed: 03 May 2019].
[7] C. M. Winkler, A. J. Dorgan and M. Mani, Scale Adaptive Simulations of Turbulent Flows on Unstructured Grids. AIAA, 2011-3559.
