Day: June 10, 2019

What We Want to Do

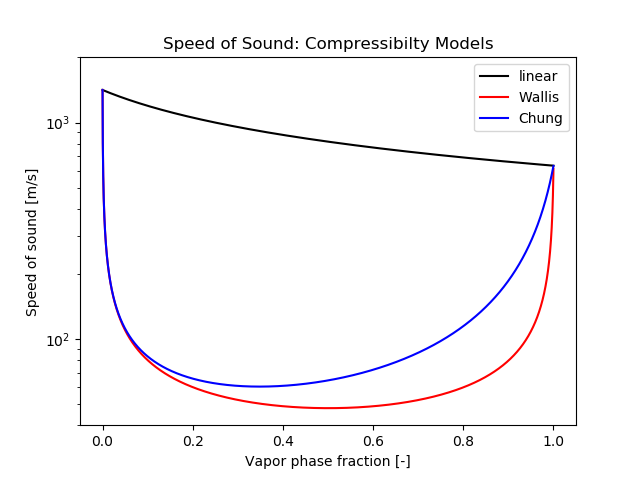
We want to plot the following three mathematical expressions in 2D that describe the speed of sound \(c\) as a function of a vapor fraction \(\gamma\).

\begin{align}
c = \frac{1}{\sqrt{\psi}}. \tag{1} \label{eq:psi-sos}
\end{align}

• • linear

\begin{align}
\psi_{linear} = \gamma \psi_v + \left(1 – \gamma \right)\psi_l \tag{2} \label{eq:linear}
\end{align}

• • Wallis

\begin{align}
\psi_{Wallis} = \left( \gamma \rho_{v, Sat} + \left( 1 – \gamma \right)\rho_{l, Sat} \right)
\left( \gamma \frac{\psi_v}{\rho_{v, Sat}} + \left( 1 – \gamma \right)\frac{\psi_l}{\rho_{l, Sat}} \right) \tag{3} \label{eq:wallis}
\end{align}

• • Chung

\begin{align}
\psi_{Chung} = \left( \left( \frac{1 – \gamma}{\sqrt{\psi_v}} + \gamma \frac{s_{fa}}{\sqrt{\psi_l}} \right)\frac{\sqrt{\psi_v \psi_l}}{s_{fa}} \right)^2 \tag{4} \label{eq:chung}
\end{align}
where
\begin{align}
s_{fa} = \sqrt{ \frac{\frac{\rho_{v, Sat}}{\psi_v}}{\left( 1- \gamma \right)\frac{\rho_{v, Sat}}{\psi_v} + \gamma \frac{\rho_{l, Sat}}{\psi_l}} } \tag{5} \label{eq:chung-sfa}
\end{align}

For more details of the above expressions, you might want to read the following post.

cavitatingFoam – barotropicCompressibilityModel (v1812)

Explanations of the barotropicCompressibilityModel of cavitatingFoam: liner, Chung and Wallis models

Sample Code