Day: June 3, 2019

Last Updated: June 9, 2019

The cavitatingFoam is a transient cavitation solver based on the homogeneous equilibrium model (HEM) from which the compressibility of the liquid/vapour ‘mixture’ is obtained, whose density varies from liquid density to vapor one according to the chosen barotropic equation of state.

Compressibility and speed of sound

\begin{align}
\frac{D \rho}{Dt} = \psi \frac{Dp}{Dt} \tag{1} \label{eq:eos}
\end{align}

\begin{align}
\psi = \rho \beta_s \tag{2} \label{eq:psi}
\end{align}

• \(\rho\): density
• \(p\): pressure
• \(\beta_s\): isentropic compressibility

The definition of the isentropic compressibility can be deformed in the following way:
\begin{align}
\beta_s &\equiv -\frac{1}{V} \left( \frac{\partial V}{\partial p} \right)_s \tag{3} \label{eq:betas} \\
&= -\frac{1}{V} \left(\frac{\partial V}{\partial \rho} \frac{\partial \rho}{\partial p} \right)_s \\
&= \rho \frac{1}{\rho^2} \left(\frac{\partial \rho}{\partial p} \right)_s \\
&= \frac{1}{\rho c^2}
\end{align}
where \(c\) is the speed of sound. We can substitute this expression for \(\beta_s\) in \eqref{eq:psi}, obtaining the following expression:
\begin{align}
\psi = \frac{1}{c^2}. \tag{4} \label{eq:psi-sos}
\end{align}
The compressibility of the mixture equals to the reciprocal of the square of the speed of sound.

We can specify a compressibility function \(\psi\) that defines the coupling between the density and pressure in the thermophysicalProperties file.

barotropicCompressibilityModel

The following three models for \(\psi\) are available in OpenFOAM v1812.

• linear
• Chung
• Wallis

• psiv: compressibility \(\psi\) of the vapor phase
• psil: compressibility \(\psi\) of the liquid phase
• pSat: saturation pressure
• rhovSat: density of vapor at saturation point
• rholSat: density of liquid at saturation point

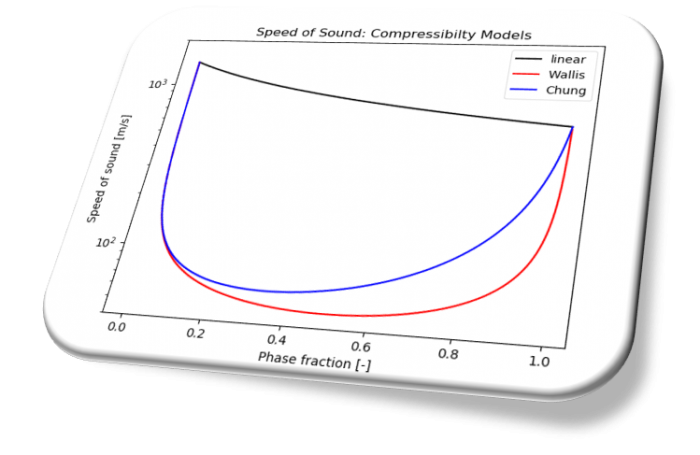
The expressions of the speed of sound \(c\) in the liquid/vapour mixture are different according to the selected function.

linear

\begin{align}
\psi = \gamma \psi_v + \left(1 – \gamma \right)\psi_l \tag{5} \label{eq:linear}
\end{align}

Chung

\begin{align}
s_{fa} = \sqrt{ \frac{\frac{\rho_{v, Sat}}{\psi_v}}{\left( 1- \gamma \right)\frac{\rho_{v, Sat}}{\psi_v} + \gamma \frac{\rho_{l, Sat}}{\psi_l}} } \tag{6} \label{eq:chung-sfa}
\end{align}
\begin{align}
\psi = \left( \left( \frac{1 – \gamma}{\sqrt{\psi_v}} + \gamma \frac{s_{fa}}{\sqrt{\psi_l}} \right)\frac{\sqrt{\psi_v \psi_l}}{s_{fa}} \right)^2 \tag{7} \label{eq:chung}
\end{align}

Wallis

\begin{align}
\psi = \left( \gamma \rho_{v, Sat} + \left( 1 – \gamma \right)\rho_{l, Sat} \right)
\left( \gamma \frac{\psi_v}{\rho_{v, Sat}} + \left( 1 – \gamma \right)\frac{\psi_l}{\rho_{l, Sat}} \right) \tag{8} \label{eq:wallis}
\end{align}
\begin{align}
\frac{\psi}{\gamma \rho_{v, Sat} + \left( 1 – \gamma \right)\rho_{l, Sat}} = \gamma \frac{\psi_v}{\rho_{v, Sat}} + \left( 1 – \gamma \right)\frac{\psi_l}{\rho_{l, Sat}} \tag{8′} \label{eq:wallis2}
\end{align}

References

[1] Christopher Earls Brennen, Fundamentals of Multiphase Flow. Cambridge University Press (2005)