Large Eddy Simulation (LES) is one of the most promising methods for computing industry-relevant turbulent flows. It is used to predict unsteady flow behaviors with lower computational cost as compared to Direct Numerical Simulation (DNS).
The essential idea of LES dates back to Joseph Smagorinsky (1963) in meteorology and to James W. Deardorff (1970) in engineering.
Keywords
Inertial subrange, Wall-modeled LES, Wall-resolved LES, Smagorinsky, Taylor microscale
Nomenclature – Abbreviations
- LES: Large Eddy Simulation
- ILES: Implicit Large Eddy Simulation
- MILES: Monotone Integrated Large Eddy Simulation
- VLES: Very Large Eddy Simulation
- WMLES: Wall-Modeled Large Eddy Simulation
- SGS: subgrid-scale
- WALE: Wall-Adapting Local Eddy-Viscosity
What is Large Eddy Simulation?
Professor Parviz Moin of Stanford University briefly explains what LES is in his interview. I’m surprised that he received his Masters and Ph.D. degrees in Mathematics and Mechanical Engineering from Stanford in the same year (1978)!
The verification of LES simulations is difficult because both the error induced by the SGS model and the numerical discretization error are dependent on the grid resolution. In the following presentation (37:40-42:06), he introduces one method using explicit filtering to distinguish the errors [6]:
If the grid-independent solution of the explicit filtered LES equations fails to accurately predict the filtered DNS flow field, its failure can be solely attributed to the capability of the subgrid stress model employed.
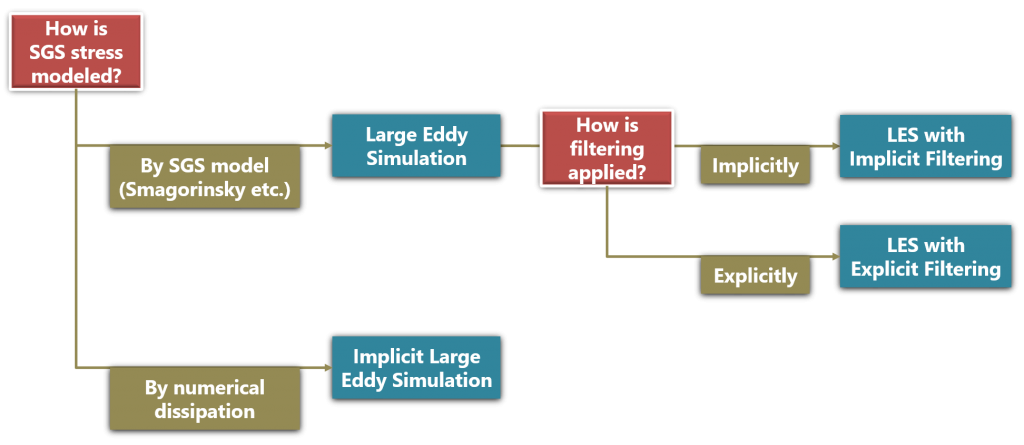
Categorization of LES
LES can be classified in terms of the following points as shown in Fig. 1:
- How the effect of the SGS stress is modeled
- How the spatial filtering is applied in the solution procedure.
In OpenFOAM, LES with the implicit filtering is implemented, in which only the filter width is specified and the filter shape is not. There exists this ambiguity in the definition of the filter. Lund [7] provides a clear description of the implicit filtering in LES:
The nearly universal approach is to simply write down the filtered Navier-Stokes equations together with an assumed model for the subgrid-scale stresses and then apply the desired spatial discretization to this “filtered” system. Although it is rarely mentioned, what one is doing by adopting this procedure is to imagine that the finite support of the computational mesh together with the low-pass characteristics of the discrete differentiating operators act as an effective filter. One then directly associates the computed velocity field with the filtered velocity. This procedure will be referred to as implicit filtering since an explicit filtering operation never appears in the solution procedure.
The explicit filtering methodology aims to damp the error-prone length scales smaller than the filter width that can be generated by the nonlinear convective term. In the case of the implicit filtering, we hope that this error has little effect on the resolved scales.
Subgrid-scale (SGS) model
SGS models in OpenFOAM
- Smagorinsky
Smagorinsky SGS model
- kEqn
One equation eddy-viscosity model
- dynamicLagrangian
Dynamic SGS model with Lagrangian averaging
- dynamicKEqn
Dynamic one equation eddy-viscosity model
- WALE
Wall-adapting local eddy-viscosity (WALE) SGS model
- DeardorffDiffStress
Differential SGS Stress Equation Model
For the dynamic SGS models, the spatial averaging operations of the coefficients are often performed to stabilize the calculation. The homogeneousDynSmagorinsky model that had been implemented in older versions takes the average of the coefficient in the whole computational domain.
Other SGS models
- Vreman SGS model [3]
\begin{equation}
\nu_{sgs} = c \sqrt{\frac{B_{\beta}}{\alpha_{ij}\alpha_{ij}}}
\end{equation}
Calculation of filter width in OpenFOAM
The method for calculating the filter width \(\Delta\) is specified in the turbulenceProperties file. The available options in OpenFOAM are as follows:
- cubeRootVol
- maxDeltaxyz
- maxDeltaxyzCubeRoot
- smooth
- vanDriest
- Prandtl
- IDDESDelta
Grid resolution measures
The choice of the computational grid size has sensible impact on the quality of the LES simulations and there are several techniques to assess the grid resolution in the LES computations [4].
- Estimations based on prior RANS results
- Single-grid estimators
- Multi-grid estimators
Principal use
- Aeroacoustics
- Aerodynamics
- Combustion
Refereces
[1] W. Rodi, J. H. Ferziger, M. Breuer and M. Pourquié, Status of Large Eddy Simulation: Results of a Workshop. Journal of Fluids Engineering, 119(2), 248-262, 1997.
[2] P. Comte, Large eddy simulations and subgrid scale modelling of turbulent shear flows
[3] A. W. Vreman, An eddy-viscosity subgrid-scale model for turbulent shear flow: Algebraic theory and applications. Physics of Fluids, 16(10), 2004.
[4] S. E. Gant, Reliability Issues of LES-Related Approaches in an Industrial Context. Flow, turbulence and combustion, 84(2), 325-335, 2010.
[5] U. Piomelli, Large eddy simulations in 2030 and beyond. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 372(2022), 2014.
[6] S. T. Bose, P. Moin and D. You, Grid-independent large-eddy simulation using explicit filtering. Center for Turbulence Research Annual Research Briefs 2008.
[7] T. S. Lund, The Use of Explicit Filters in Large Eddy Simulation. Computers and Mathematics with Applications 46, 603-616, 2003.
Refereces (Japanese)
List of Laboratories
- Center for Turbulence Research (Stanford University)
Professor Parviz Moin is the founding director of the Center for Turbulence Research at Stanford and the co-founder of Cascade Technologies that develops CHARLES, a high-fidelity unstructured compressible flow solver for Large Eddy Simulation.
I am working with LES SGS models and want to implement anisotropic filter with dynamic one equation model. But I am getting error while I am specifying the widthCoeff. What is this widthCoeff here, is a multiple of delta or direct value of grid size. Here is the syntex:
dynOneEqEddyCoeffs
{
filter anisotropic ;
anisotropic Coeffs
{
widthCoeff 0.0004;
}
}