Month: April 2017

Hyperbolic tangent function to create stretched grid


Hyperbolic tangent function \({\rm tanh}\) is often used to generate the stretched structured grid.

In this blog post, I will introduce some examples I have found in the references.

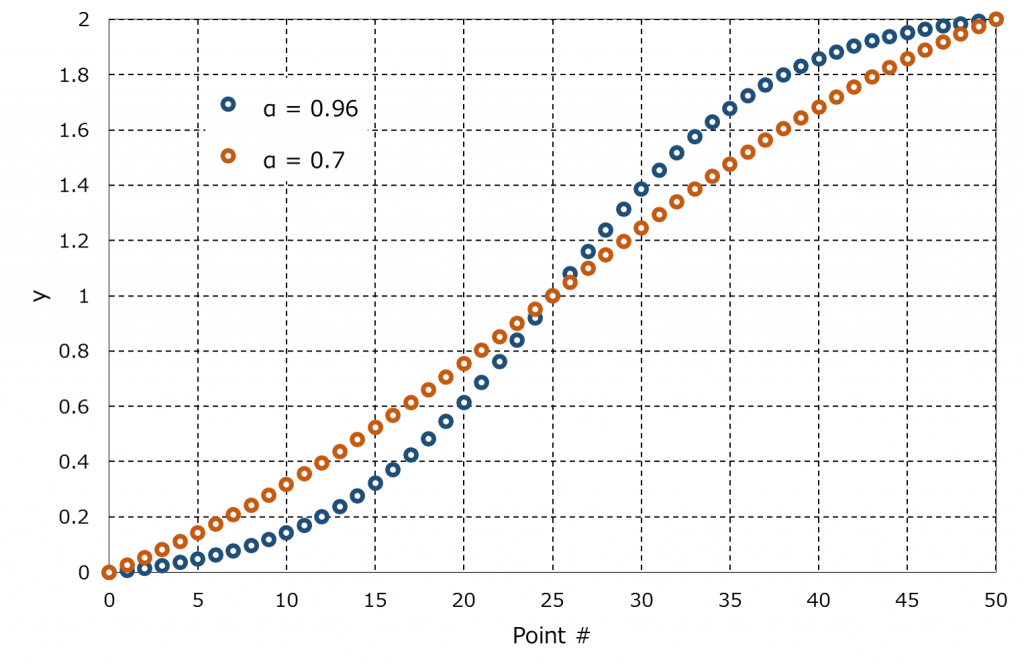
Example #1 [1]

\begin{equation}
y_j = \frac{1}{\alpha}{\rm tanh} \left[\xi_j {\rm tanh}^{-1}\left(\alpha\right)\right] + 1\;\;\;\left( j = 0, …, N_2 \right), \tag{1}
\end{equation}
with
\begin{equation}
\xi_j = -1 + 2\frac{j}{N_2}, \tag{2}
\end{equation}
where \(\alpha\) is an adjustable parameter of the transformation \((0<\alpha<1)\) and \(N_2\) is the grid number of the direction. As shown in the following figure, the grids are more clustered towards the both ends as the parameter \(\alpha\) approaches 1.

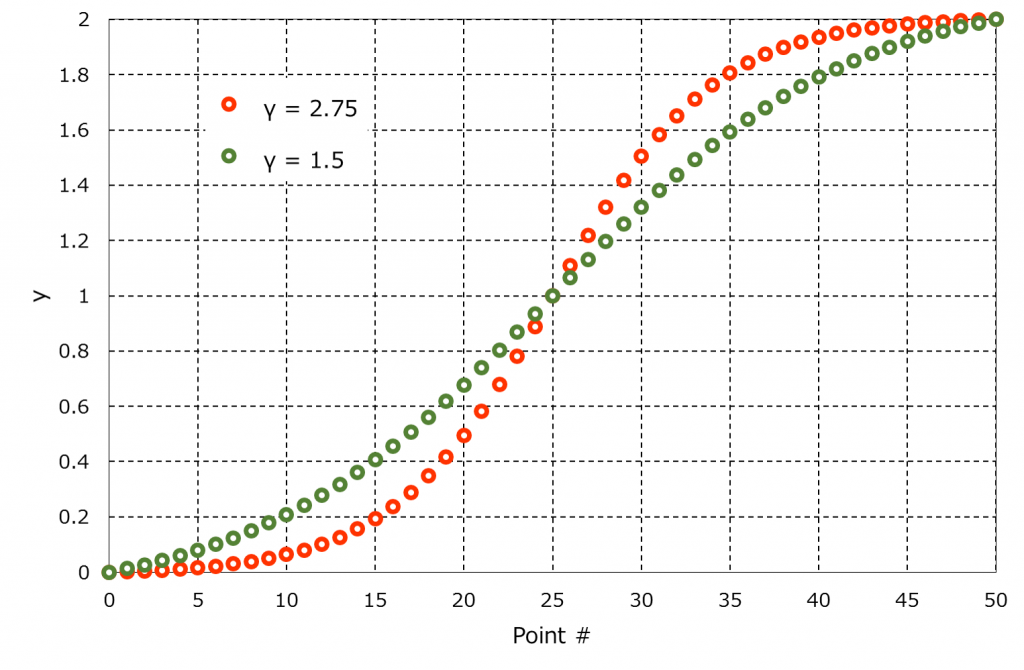
Example #2 [2]

\begin{equation}
y_j = 1 -\frac{{\rm tanh}\left[ \gamma \left( 1 – \frac{2j}{N_2} \right) \right]}{{\rm tanh} \left( \gamma \right)}\;\;\;\left( j = 0, …, N_2 \right), \tag{3}
\end{equation}
where \(\gamma\) is the stretching parameter and \(N_2\) is the number of grid points of the direction.

Grid Images

Coming soon.

References

[1] H. Abe, H. Kawamura and Y. Matsuo, Direct Numerical Simulation of a Fully Developed Turbulent Channel Flow With Respect to the Reynolds Number Dependence. J. Fluids Eng 123(2), 382-393, 2001.
[2] J. Gullbrand, Grid-independent large-eddy simulation in turbulent channel flow using three-dimensional explicit filtering. Center for Turbulence Research Annual Research Briefs, 2003.

Calculation of Reynolds stress field in OpenFOAM


Keywords
Reynolds stress, shear flow, fieldAverage, variance, covariance

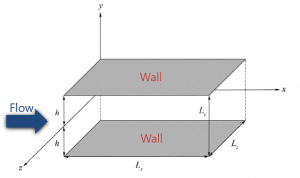
In the simulations of wall-bounded turbulent flows, such as turbulent channel flow [1], the distributions of the Reynolds stress components in the wall-normal direction are matters of interest to researchers and engineers.

For a statistically steady turbulent flow, a prime-squared mean of the velocity field (UPrime2Mean in OpenFOAM) gives the Reynolds stress field

\begin{eqnarray}
\frac{1}{N} \sum_{k=1}^{N} \left( U_i^{(k)} – \overline{U_i} \right)^2
&=& \frac{1}{N} \sum_{k=1}^{N} {u_{i}^{(k)}}^2 \\
&=& \frac{1}{N} \sum_{k=1}^{N}
\left[
\begin{array}{ccc}
u_{1}^{(k)}u_{1}^{(k)} & u_{1}^{(k)}u_{2}^{(k)} & u_{1}^{(k)}u_{3}^{(k)} \\
u_{2}^{(k)}u_{1}^{(k)} & u_{2}^{(k)}u_{2}^{(k)} & u_{2}^{(k)}u_{3}^{(k)} \\
u_{3}^{(k)}u_{1}^{(k)} & u_{3}^{(k)}u_{2}^{(k)} & u_{3}^{(k)}u_{3}^{(k)}
\end{array}
\right] \\
&=&
\left[
\begin{array}{ccc}
\overline{u_{1}u_{1}} & \overline{u_{1}u_{2}} & \overline{u_{1}u_{3}} \\
\overline{u_{2}u_{1}} & \overline{u_{2}u_{2}} & \overline{u_{2}u_{3}} \tag{1} \\
\overline{u_{3}u_{1}} & \overline{u_{3}u_{2}} & \overline{u_{3}u_{3}}
\end{array}
\right], \\
\end{eqnarray}

where \(U_i^{(k)}\) denotes the instantaneous velocity field \(U_i(\boldsymbol{x}, k\Delta t)\) and it is decomposed into the time-averaged mean \(\overline{U_i}\) and fluctuating components \({u_{i}}^{(k)}\),
\begin{equation}
{U_{i}}^{(k)} = \overline{U_i} + {u_{i}}^{(k)}. \tag{2}
\end{equation}

The diagonal components of the Reynolds stress tensor are the variances of the velocity components and the off-diagonal elements are the covariances of them.

Function Object – fieldAverage

Turbulent Channel Flow

Turbulent channel flow is one of the most fundamental wall-bounded shear flows and it has been widely used to study the structure of near-wall turbulence. Many DNS calculations have been carried out and produced a lot of informative data, which has contributed considerably to the improvements of other turbulence models, such as RANS and LES.

Moser et al. have released the statistical data obtained from their DNS of turbulent channel flow on their web site [2]. The data set contains, among other information, the components of the Reynolds stress tensor at three Reynolds numbers
\begin{equation}
Re_{\tau} = \frac{u_{\tau}h}{\nu} \approx 180,\; 395,\; 590, \tag{3}
\end{equation}
where \(u_{\tau}\) is the friction velocity, \(h\) is the channel half-height and \(\nu\) is the kinematic viscosity.

I will post my DNS results, which will help us to understand the flow behaviors in the near-wall region. The channel395 tutorial in OpenFOAM is the case of large eddy simulation (LES) instead of DNS at \(Re_{\tau}=395\).

References

[1] R. D. Moser, J. Kim and N. N. Mansour, Direct numerical simulation of turbulent channel flow up to \({\rm Re}_{\tau}\)=590. Physics of Fluids 11(4), 943-945, 1999.
[2] DNS Data for Turbulent Channel Flow. Available at: http://turbulence.ices.utexas.edu/data/MKM/ [Accessed: 9 April 2017].
[3] turbulence.ices.utexas.edu file server. Available at: http://turbulence.ices.utexas.edu/ [Accessed: 4 May 2017].