In this blog post, I will try to give a description of the governing equation of the laplacianFoam in OpenFOAM that solves a simple Laplace equation, e.g. for thermal diffusion in a solid.
| Governing Equation |
The heat conduction equation is given by the following equation:
\begin{align}
\frac{\partial T}{\partial t} = \frac{1}{\rho c_p} \nabla \cdot \left(k \nabla T\right) + \frac{q}{\rho c_p}, \tag{1} \label{eq:conductionEqn}
\end{align}
where \(T\;{\rm [ K]}\) is the absolute temperature field, \(\rho\;{\rm [kg/m^3]}\) is the density field, \(q\;{\rm [W/m^3]}\) is the rate of energy generation per unit volume, \(k\;{\rm [W/(m\cdot K)]}\) is the thermal conductivity and \(c_p\;{\rm [J/(kg\cdot K)]}\) is the specific heat at constant pressure.
If the heat capacity \(\rho c_p\) is spatially uniform, the Eq. \eqref{eq:conductionEqn} can be transformed into the following form irrespective of whether the thermal conductivity \(k\) is spatially uniform or not:
\begin{align}
\frac{\partial T}{\partial t} = \nabla \cdot \left(\alpha \nabla T\right) + \frac{q}{\rho c_p}, \tag{2} \label{eq:conductionEqn2}
\end{align}
where \(\alpha = k/\rho c_p\;{\rm [m^2/s]}\) is the thermal diffusivity.
The laplacianFoam (in OpenFOAM-4.x and earlier versions) doesn’t consider the heat generation and the implemented equation is
\begin{align}
\frac{\partial T}{\partial t} = \nabla \cdot \left(\alpha \nabla T\right), \tag{3} \label{eq:laplacianFoam}
\end{align}
but the solver in the latest development version supports the fvOptions so that we can solve \eqref{eq:conductionEqn2} and specify a volumetric heat source.
We can find the Eq. \eqref{eq:conductionEqn2} solved in laplacianFoam.C.
|
58 59 60 61 62 63 64 65 66 67 68 69 70 |
while (simple.correctNonOrthogonal()) { fvScalarMatrix TEqn ( fvm::ddt(T) - fvm::laplacian(DT, T) == fvOptions(T) ); fvOptions.constrain(TEqn); TEqn.solve(); fvOptions.correct(T); } |
The variable DT represents the thermal diffusivity \(\alpha\) and it is specified in the constant/transportProperties file.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
FoamFile { version 2.0; format ascii; class dictionary; location "constant"; object transportProperties; } // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // DT DT [0 2 -1 0 0 0 0] 4e-05; // thermal diffusivity m^2/s // ************************************************************************* // |
| Comparison with Analytical Solution |
We consider the steady state problem of source-free heat conduction in a concentric cylinder whose inner and outer walls are maintained at constant temperature of 400 K and 300 K respectively. This problem can be analytically solved and the following relation holds for the temperature distribution in the radial direction \(T(r)\):
\begin{align}
\frac{T_1 – T(r)}{T_1 – T_2} = \frac{\ln{(r/r_1)}}{\ln{(r_2/r_1)}}, \tag{4} \label{eq:cylinderT}
\end{align}
where the subscripts 1 and 2 indicate the values at the inner and outer walls respectively shown in Figure 1.
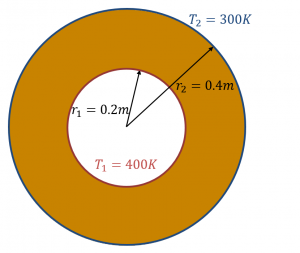
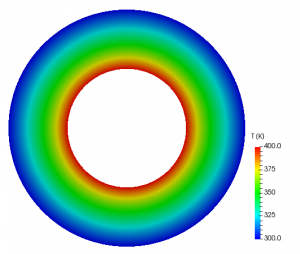
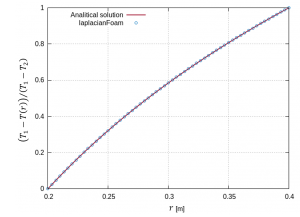
The temperature distribution obtained using laplacianFoam is shown in Figure 2 and the comparison between the numerical and analytical solutions is shown in Figure 3. The agreement with the analytical solution is good.
| Introduction of Source Term |
In the next post, I’ll deal with a simple example case to introduce how to specify a heat generation source term in laplacianFoam using the fvOptions functionality (scalarSemiImplicitSource).