Last Updated: May 3, 2019
For accurate computational aeroacoustics (CAA) simulations, we have to prevent the acoustic waves from reflecting on the truncated boundary of the computational domain so that the reflected waves will not contaminate the acoustic field by wave interference.
A variety of numerical techniques have been developed for this purpose. In this blog post, I will try to give a description of one of these methods, namely the artificial damping (dissipation) method.
General Description
This damping method is briefly described in [1].
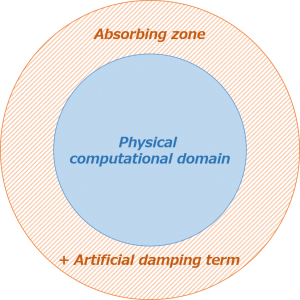
In this method, an absorbing zone is created and appended to the physical computational domain in which the governing equations are modified to mimic a physical dissipation mechanism.
For the Euler and Navier-Stokes equations, the artificial damping term can easily be introduced into the governing equations as follows:
\begin{align}
\frac{\partial \boldsymbol{u}}{\partial t} = L(\boldsymbol{u})\; – \nu(\boldsymbol{u} – \boldsymbol{u}_0), \tag{5.155} \label{eq:damping}
\end{align}where \(\boldsymbol{u}\) is the solution vector and \(L(\boldsymbol{u})\) denotes the spatial operators of the equations. The damping coefficient \(\nu\) assumes a positive value and should be increased slowly inside the zone. Here, \(\boldsymbol{u}_0\) is the time-independent mean value in the absorbing zone (Freund 1997). Kosloff and Kosloff (1986) analyzed a system similar to Equation \eqref{eq:damping} for the two-dimensional wave equation in which, in particular, a reflection coefficient of a multilayer absorbing zone was calculated.
The role of the artificial damping term is to diminish the strength of the waves in the absorbing zone before they reach the truncated boundary and to minimize the reflecting effect.
Settings of acousticDampingSource
In OpenFOAM v1606+, this artificial damping method is available as the newly implemented fvOption acousticDampingSource [2]. Its settings are described in the system/fvOptions file.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 |
/*--------------------------------*- C++ -*----------------------------------*\ | ========= | | | \\ / F ield | OpenFOAM: The Open Source CFD Toolbox | | \\ / O peration | Version: plus | | \\ / A nd | Web: www.OpenFOAM.com | | \\/ M anipulation | | \*---------------------------------------------------------------------------*/ FoamFile { version 2.0; format ascii; class dictionary; location "system"; object fvOptions; } // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // acousticDampingSource { type acousticDampingSource; active yes; acousticDampingSourceCoeffs { timeStart 0.004; duration 1000.0; selectionMode all; centre (-1.25 0 0); radius1 1.2; radius2 1.65; frequency 3000; w 20; URef UMean; } } //************************************************************************* // |
- timeStart: [Optional] Start time
- duration: [Optional] Duration time
- selectionMode: [Required] Domain where the source is applied (all/cellSet/cellZone/points)
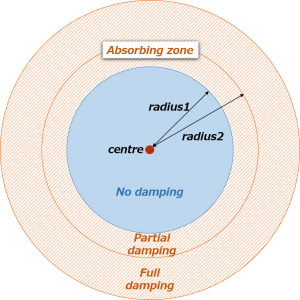
- centre: [Required] Sphere centre location of damping
- radius1: [Required] Inner radius at which to start damping
- radius2: [Required] Outer radius beyond which full damping is applied
- frequency: [Required] Frequency [Hz]
- w: [Optional] Stencil width (default = 20)
- Uref: [Required] Name of reference velocity field
The strength of damping is gradually increased from radius1 to radius2 and full damping is applied in the region where \(r >\) radius2. The maximum value of damping coefficient is defined as follows:
\begin{align}
\nu_{max} = w \times frequency. \tag{1} \label{eq:maxnu}
\end{align}
This function is only applicable for the momentum equation by default, so it needs source modifications so that it can be used in the mass and energy conservation equations as well.
An Example in 1D (Plane Wave)
Sound waves are longitudinal waves but I intentionally visualize them like the transverse waves in order to make the damping effect more visible in the following video. The damping is activated at time = 0.004s.
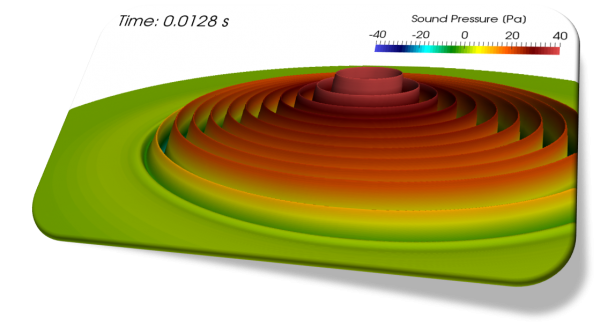
An Example in 2D (Cylindrical Wave)
Sound waves are longitudinal waves but I intentionally visualize them like the transverse waves in order to make the damping effect more visible in the following video. The damping is activated at time = 0.004s.
The amplitude gets smaller as they propagate from a sound source in contrast to the plane waves (cylindrical spreading).
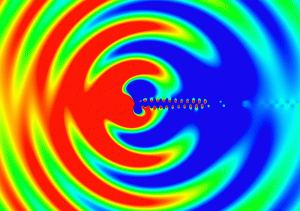
Aeolian Tone
Source Code
The damping source terms added to the incompressible and compressible momentum equations are calculated by Eq. \eqref{eq:damping} in addSup function.
|
121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 |
void Foam::fv::acousticDampingSource::addSup ( fvMatrix<vector>& eqn, const label fieldI ) { const volVectorField& U = eqn.psi(); const volScalarField coeff(name_ + ":coeff", w_*frequency_*blendFactor_); const volVectorField& URef(mesh().lookupObject<volVectorField>(URefName_)); fvMatrix<vector> dampingEqn ( fvm::Sp(coeff, U) - coeff*URef ); eqn -= dampingEqn; } void Foam::fv::acousticDampingSource::addSup ( const volScalarField& rho, fvMatrix<vector>& eqn, const label fieldI ) { const volVectorField& U = eqn.psi(); const volScalarField coeff(name_ + ":coeff", w_*frequency_*blendFactor_); const volVectorField& URef(mesh().lookupObject<volVectorField>(URefName_)); fvMatrix<vector> dampingEqn ( fvm::Sp(rho*coeff, U) - rho*coeff*URef ); eqn -= dampingEqn; } |
The profile of damping coefficient in the radial direction is calculated by the trigonometric (cosine) function in setBlendingFactor helper function.
|
53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 |
void Foam::fv::acousticDampingSource::setBlendingFactor() { blendFactor_.internalField() = 1; const vectorField& Cf = mesh_.C(); const scalar pi = constant::mathematical::pi; forAll(cells_, i) { label celli = cells_[i]; scalar d = mag(Cf[celli] - x0_); if (d < r1_) { blendFactor_[celli] = 0.0; } else if ((d >= r1_) && (d <= r2_)) { blendFactor_[celli] = (1.0 - cos(pi*mag(d - r1_)/(r2_ - r1_)))/2.0; } } blendFactor_.correctBoundaryConditions(); } |
References
- [1] Claus Albrecht Wagner et al., Large-Eddy Simulation for Acoustics (Cambridge Aerospace Series)
- [2] OpenFOAM® v1606+: New Solvers. Available at: https://www.openfoam.com/releases/openfoam-v1606+/solvers-and-physics.php#solvers-and-physics-acoustic-damping [Accessed: 03 May 2019].
Dear Mr. Fumiya
Thank you for your very helpful article. Currently I am also running a similar simulation to Aeolian Tone.
But unfortunately I cannot understand how it is possible that the sound radiation in the rectangular CFD domain can be radiated without reflection on the wall.
If you set two radii of acoustic damping, the pressure fluctuations out of radius2 must be completely zero?
Sincerely yours,
C. Jeong