Thermal Boundary Conditions in OpenFOAM

Many thermal boundary conditions are available in OpenFOAM.
I will upload some basic cases that explain the usage of these boundary conditions.

Source Code
src/TurbulenceModels/compressible/turbulentFluidThermoModels/derivedFvPatchFields/

• convectiveHeatTransfer

  It calculates the heat transfer coefficients from the following empirical correlations for forced convection heat transfer:
  \begin{eqnarray}
  \left\{
  \begin{array}{l}
  Nu = 0.664 Re^{\frac{1}{2}} Pr^{\frac{1}{3}} \left( Re \lt 5 \times 10^5 \right) \\
  Nu = 0.037 Re^{\frac{4}{5}} Pr^{\frac{1}{3}} \left( Re \ge 5 \times 10^5 \right) \tag{1} \label{eq:NuPlate}
  \end{array}
  \right.
  \end{eqnarray}
  where \(Nu\) is the Nusselt number, \(Re\) is the Reynolds number and \(Pr\) is the Prandtl number.

• externalCoupledTemperature
• externalWallHeatFluxTemperature

  This boundary condition can operate in the following two modes:
  Mode#1 Specify the heat flux \(q\)
  \begin{equation}
  -k \frac{T_p – T_b}{\vert \boldsymbol{d} \vert} = q + q_r \tag{2} \label{eq:fixedHeatFlux}
  \end{equation}
  * \(k\): thermal conductivity
  * \(q_r\): radiative heat flux
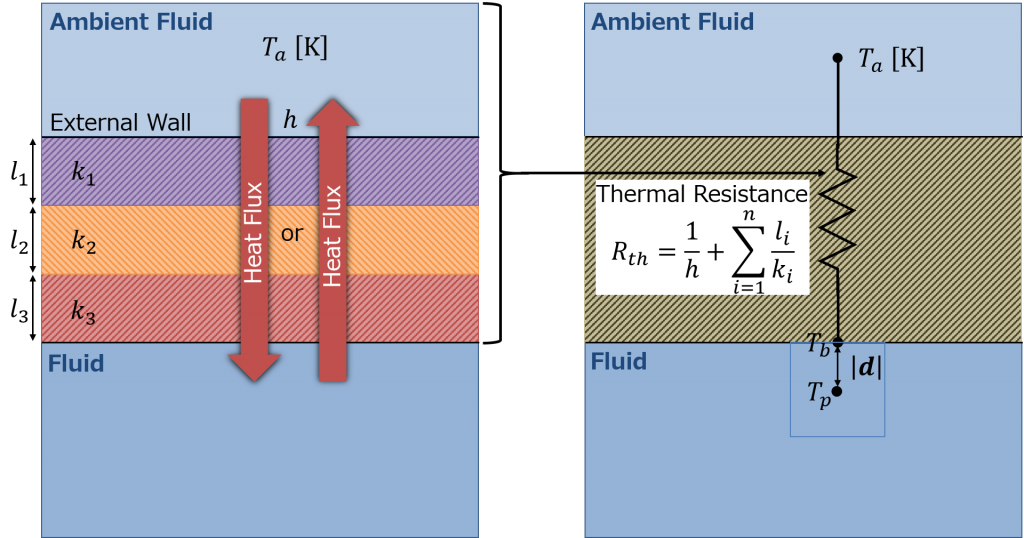
  * \(T_b\): temperature on the boundary

  Mode#2 Specify the heat transfer coefficient \(h\) and the ambient temperature \(T_a\) (Fig. 1)
  \begin{equation}
  -k \frac{T_p – T_b}{\vert \boldsymbol{d} \vert} = \frac{T_a – T_b}{R_{th}} + q_r \tag{3} \label{eq:fixedHeatTransferCoeff}
  \end{equation}
  * \(R_{th}\): total thermal resistance of convective and conductive heat transfer
  \begin{equation}
  R_{th} = \frac{1}{h} + \sum_{i=1}^{n} \frac{l_i}{k_i} \tag{4} \label{eq:Rth}
  \end{equation}

  

• fixedIncidentRadiation
• lumpedMassWallTemperature

  There is a dimensionless quantity called the Biot number, which is defined as
  \begin{equation}
  Bi = \frac{l/k}{1/h} = \frac{hl}{k}, \tag{5} \label{eq:Biot}
  \end{equation}
  where \(h\) is the heat transfer coefficient, \(k\) is the thermal conductivity of a solid and \(l\) is the characteristic length of the solid. As the definition in Eq. \eqref{eq:Biot} indicates, it represents the ratio of the internal conduction resistance \(l/k\) and the external convection resistance \(1/h\). If the Biot number is small (\(Bi \ll 1\)), the solid may be treated as a simple lumped mass system of an uniform temperature. This boundary condition calculates the uniform temperature variation \(\Delta T\) on the boundary from the following equation:
  \begin{equation}
  m c_p \Delta T = Q \Delta t. \tag{6} \label{eq:lumpedmass}
  \end{equation}
  * \(m\): total mass [kg]
  * \(c_p\): specific heat capacity [J/(kg.K)]
  * \(Q\): net heat flux on the boundary [W]
  * \(\Delta t\): time step [s]

• outletMappedUniformInletHeatAddition
• totalFlowRateAdvectiveDiffusive
• wallHeatTransfer
• compressible::thermalBaffle1D
• compressible::turbulentHeatFluxTemperature
• compressible::turbulentTemperatureCoupledBaffleMixed
• compressible::turbulentTemperatureRadCoupledMixed
• compressible::alphatJayatillekeWallFunction
• compressible::alphatPhaseChangeWallFunction
• compressible::alphatWallFunction

Author: fumiya

CFD engineer in Japan View all posts by fumiya