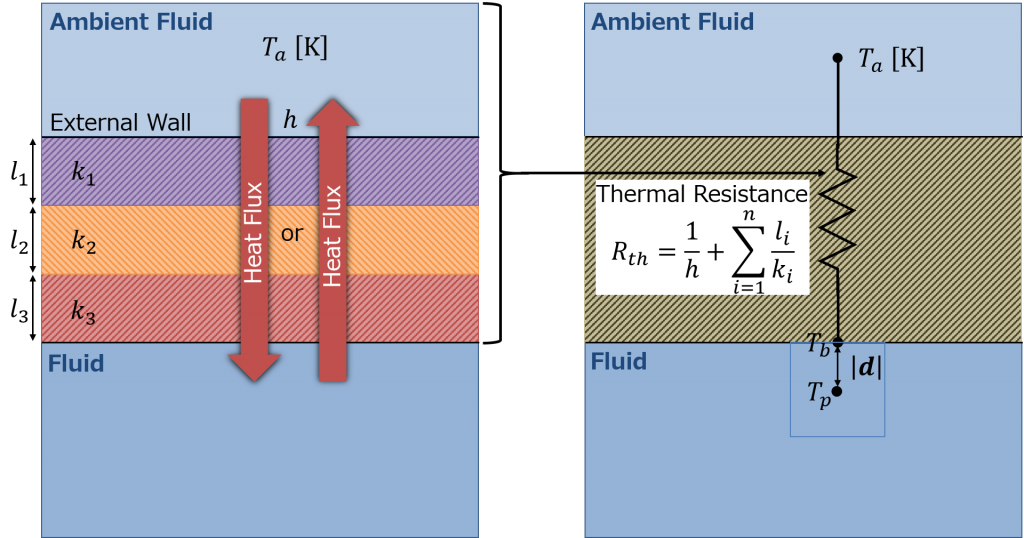
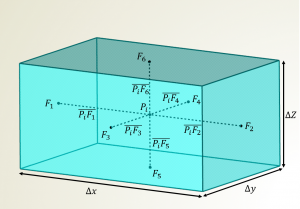
template<class BasicPsiThermo, class MixtureType>
void Foam::hePsiThermo<BasicPsiThermo, MixtureType>::calculate()
{
const scalarField& hCells = this->he_;
const scalarField& pCells = this->p_;
scalarField& TCells = this->T_.primitiveFieldRef();
scalarField& psiCells = this->psi_.primitiveFieldRef();
scalarField& muCells = this->mu_.primitiveFieldRef();
scalarField& alphaCells = this->alpha_.primitiveFieldRef();
forAll(TCells, celli)
{
const typename MixtureType::thermoType& mixture_ =
this->cellMixture(celli);
TCells[celli] = mixture_.THE
(
hCells[celli],
pCells[celli],
TCells[celli]
);
psiCells[celli] = mixture_.psi(pCells[celli], TCells[celli]);
muCells[celli] = mixture_.mu(pCells[celli], TCells[celli]);
alphaCells[celli] = mixture_.alphah(pCells[celli], TCells[celli]);
}
volScalarField::Boundary& pBf =
this->p_.boundaryFieldRef();
volScalarField::Boundary& TBf =
this->T_.boundaryFieldRef();
volScalarField::Boundary& psiBf =
this->psi_.boundaryFieldRef();
volScalarField::Boundary& heBf =
this->he().boundaryFieldRef();
volScalarField::Boundary& muBf =
this->mu_.boundaryFieldRef();
volScalarField::Boundary& alphaBf =
this->alpha_.boundaryFieldRef();
forAll(this->T_.boundaryField(), patchi)
{
fvPatchScalarField& pp = pBf[patchi];
fvPatchScalarField& pT = TBf[patchi];
fvPatchScalarField& ppsi = psiBf[patchi];
fvPatchScalarField& phe = heBf[patchi];
fvPatchScalarField& pmu = muBf[patchi];
fvPatchScalarField& palpha = alphaBf[patchi];
if (pT.fixesValue())
{
forAll(pT, facei)
{
const typename MixtureType::thermoType& mixture_ =
this->patchFaceMixture(patchi, facei);
phe[facei] = mixture_.HE(pp[facei], pT[facei]);
ppsi[facei] = mixture_.psi(pp[facei], pT[facei]);
pmu[facei] = mixture_.mu(pp[facei], pT[facei]);
palpha[facei] = mixture_.alphah(pp[facei], pT[facei]);
}
}
else
{
forAll(pT, facei)
{
const typename MixtureType::thermoType& mixture_ =
this->patchFaceMixture(patchi, facei);
pT[facei] = mixture_.THE(phe[facei], pp[facei], pT[facei]);
ppsi[facei] = mixture_.psi(pp[facei], pT[facei]);
pmu[facei] = mixture_.mu(pp[facei], pT[facei]);
palpha[facei] = mixture_.alphah(pp[facei], pT[facei]);
}
}
}
}