Several options are available in OpenFOAM for calculation of the filter width used in the large eddy simulation (LES) and detached eddy simulation (DES). In this blog post, the maxDeltaxyz option is covered in some detail.
OpenFOAM Version: OpenFOAM-dev, OpenFOAM v1612+
| Implementation in OpenFOAM |
The maxDeltaxyz option calculates the filter width of the \(i-\)th cell \(\Delta_i\) by taking the maximum distance between the cell center \(P_i\) and each face center \(F_j\)
\begin{equation}
\Delta_i = {\rm deltaCoeff} \times \max_{1 \le j \le n_i} \left\{ \overline{P_iF_j} \right\}, \tag{1} \label{eq:deltaxyz}
\end{equation}
where \({\rm deltaCoeff}\) is a constant of proportion (user input) and \(n_i\) is the number of the faces of the \(i-\)th cell.
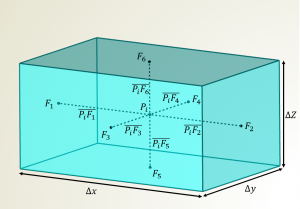
For a regular hexahedral cell shown in Fig. 1, the computed \(\Delta\) using Eq. \eqref{eq:deltaxyz} equals one-half of the maximum cell width \(\Delta x\), so the deltaCoeff coefficient should be set to 2 in the turbulenceProperties file as shown below.
|
1 2 3 4 |
maxDeltaxyzCoeffs { deltaCoeff 2; } |
The filter width is calculated in the following function.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 |
void Foam::LESModels::maxDeltaxyz::calcDelta() { const fvMesh& mesh = turbulenceModel_.mesh(); label nD = mesh.nGeometricD(); const cellList& cells = mesh.cells(); scalarField hmax(cells.size()); forAll(cells,celli) { scalar deltaMaxTmp = 0.0; const labelList& cFaces = mesh.cells()[celli]; const point& centrevector = mesh.cellCentres()[celli]; forAll(cFaces, cFacei) { label facei = cFaces[cFacei]; const point& facevector = mesh.faceCentres()[facei]; scalar tmp = mag(facevector - centrevector); if (tmp > deltaMaxTmp) { deltaMaxTmp = tmp; } } hmax[celli] = deltaCoeff_*deltaMaxTmp; } if (nD == 3) { delta_.primitiveFieldRef() = hmax; } else if (nD == 2) { WarningInFunction << "Case is 2D, LES is not strictly applicable\n" << endl; delta_.primitiveFieldRef() = hmax; } else { FatalErrorInFunction << "Case is not 3D or 2D, LES is not applicable" << exit(FatalError); } } |
| Implementation in OpenFOAM v1612+ |
In OpenFOAM v1612+, the face normal vectors are considered in order to take into account the mesh non-orthogonality.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 |
void Foam::LESModels::maxDeltaxyz::calcDelta() { const fvMesh& mesh = turbulenceModel_.mesh(); label nD = mesh.nGeometricD(); const cellList& cells = mesh.cells(); const vectorField& cellC = mesh.cellCentres(); const vectorField& faceC = mesh.faceCentres(); const vectorField faceN(mesh.faceAreas()/mag(mesh.faceAreas())); scalarField hmax(cells.size()); forAll(cells, celli) { scalar deltaMaxTmp = 0.0; const labelList& cFaces = cells[celli]; const point& cc = cellC[celli]; forAll(cFaces, cFacei) { label facei = cFaces[cFacei]; const point& fc = faceC[facei]; const vector& n = faceN[facei]; scalar tmp = magSqr(n*(n & (fc - cc))); if (tmp > deltaMaxTmp) { deltaMaxTmp = tmp; } } hmax[celli] = deltaCoeff_*Foam::sqrt(deltaMaxTmp); } if (nD == 3) { delta_.primitiveFieldRef() = hmax; } else if (nD == 2) { WarningInFunction << "Case is 2D, LES is not strictly applicable" << nl << endl; delta_.primitiveFieldRef() = hmax; } else { FatalErrorInFunction << "Case is not 3D or 2D, LES is not applicable" << exit(FatalError); } // Handle coupled boundaries delta_.correctBoundaryConditions(); } |
| Some comments |
This definition \eqref{eq:deltaxyz} is often used in the detached eddy simulation (DES) where some anisotropic grid cells such as “book”, “pencil” and “ribbon”-shaped cells exist in a boundary layer mesh. The position where switching between the RANS and LES modes occurs in the DES97 model [1] depends on how to calculate the filter width \(\Delta\)
\begin{equation}
\tilde{d} \equiv {\rm min}\left( d, C_{DES}\Delta \right), \tag{2} \label{eq:dTilda}
\end{equation}
where \(d\) is the distance to the closest wall and \(C_{DES}\) is a calibration constant.
Several modified length scales have been developed to prevent a delay of the Kelvin-Helmholtz instability in free and separated shear layers [2].
| References |
[1] P. R. Spalart, W.-H. Jou, M. Strelets and S. R. Allmaras, Comments on the feasibility of LES for wings, and on a hybrid RANS/LES approach. 1st AFOSR Int. Conf. on DNS/LES, Aug. 4-8, 1997, Ruston, LA. In “Advances in DNS/LES”, C. Liu and Z. Liu Eds., Greyden Press, Columbus, OH.
[2] P. R. Spalart, Detached-Eddy Simulation. Annu. Rev. Fluid Mech. 41, 181-202, 2009.