Tag: RANS

Diffusion Term of the N-S Equations Part1


The mathematical expressions of the viscous stress differ between Newtonian fluids and non-Newtonian fluids, so do those of the diffusion term. In this post, we consider only Newtonian fluids, such as air and water.

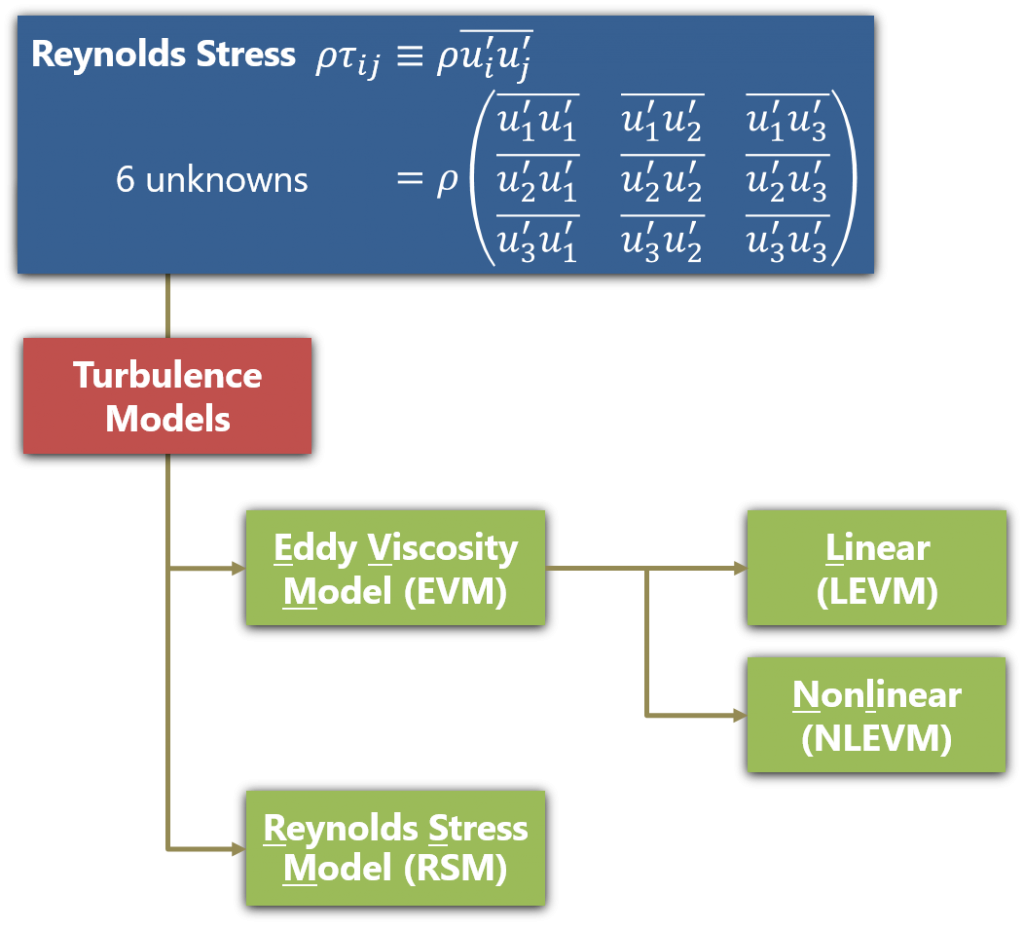
Many turbulence models treat the effects of the turbulence as augmentation of mixing or diffusion, but the modeled expression differs depending on the turbulence models, such as linear eddy-viscosity, non-linear eddy viscosity and Reynolds-stress transport models.

We’ll start by running through mathematical expressions of the diffusion term and find out how these are implemented in OpenFOAM.

Diffusion term (Newtonian fluids)

For Newtonian fluids the ratio of the shear stress to the shear rate is constant and the diffusion term of the Navier-Stokes equations are given by:

\begin{equation}
\nabla \cdot \left( \mu \left( \nabla \boldsymbol{u} + (\nabla \boldsymbol{u})^T \right) -\frac{2}{3}\mu (\nabla \cdot \boldsymbol{u}) \boldsymbol{I} \right), \tag{1} \label{eq:newtondiffusion}
\end{equation}
where \(\boldsymbol{u}\) is the velocity field, \(\mu\) is the molecular viscosity and \(\boldsymbol{I}\) is the identity tensor.

In the case of laminar flows and Direct Numerical Simulations (DNS) of turbulent flows, this expression is used.

When we solve turbulent flows with turbulence models, the expression of the diffusion term changes from Eq. \eqref{eq:newtondiffusion} according to the model we choose. If we use the linear eddy-viscosity models of Reynolds-averaged Navier-Stokes (RANS), such as k-\(\epsilon\) and k-\(\omega\) SST models, the Reynolds stress is modeled with the following expression:

\begin{equation}
-\rho\overline{\boldsymbol{u}\boldsymbol{u}} = \mu_t \left( \nabla \overline{\boldsymbol{u}} + (\nabla \overline{\boldsymbol{u}})^T \right) -\frac{2}{3}\rho k \boldsymbol{I}, \tag{2} \label{eq:BoussinesqApprox}
\end{equation}

and the diffusion term is expressed as:

\begin{align}
&\nabla \cdot \left( \mu \left( \nabla \overline{\boldsymbol{u}} + (\nabla \overline{\boldsymbol{u}})^T \right) -\frac{2}{3}\mu (\nabla \cdot \overline{\boldsymbol{u}}) \boldsymbol{I} -\rho\overline{\boldsymbol{u}\boldsymbol{u}} \right) \\
=& \nabla \cdot \left( (\mu + \mu_t) \left( \nabla \overline{\boldsymbol{u}} + (\nabla \overline{\boldsymbol{u}})^T \right) -\frac{2}{3}\mu (\nabla \cdot \overline{\boldsymbol{u}}) \boldsymbol{I} – \frac{2}{3}\rho k \boldsymbol{I} \right) \\
=& \nabla \cdot \left( \mu_{eff} \left( \nabla \overline{\boldsymbol{u}} + (\nabla \overline{\boldsymbol{u}})^T \right) -\frac{2}{3}\mu (\nabla \cdot \overline{\boldsymbol{u}}) \boldsymbol{I} \right) – \nabla \cdot \left( \frac{2}{3}\rho k \boldsymbol{I} \right), \tag{3} \label{eq:levmdiffusion}
\end{align}
where \(\overline{\boldsymbol{u}}\) is the ensemble-averaged velocity field, \(k\) is the turbulence energy, \(\rho\) is the density and the effective viscosity \(\mu_{eff}\) is the sum of the molecular and turbulent eddy viscosity \(\mu_t\).

If the flow is incompressible, the expression reduces to the following one because of the continuity equation \(\nabla \cdot \overline{\boldsymbol{u}} = 0\):
\begin{equation}
\nabla \cdot \left( \mu_{eff} \left( \nabla \overline{\boldsymbol{u}} + (\nabla \overline{\boldsymbol{u}})^T \right) \right) – \nabla \cdot \left( \frac{2}{3}\rho k \boldsymbol{I} \right). \tag{4} \label{eq:incompdiffusion}
\end{equation}

If turbulence models of the eddy-viscosity type is used, the effects of fluctuating turbulent flows are expressed as augmentation of the diffusion as can be seen from Eq. \eqref{eq:levmdiffusion}.

We are all set!
Let’s look into how the diffusion term is handled in OpenFOAM 🙂

Implementation in OpenFOAM

If we have a quick look at UEqn.H file of rhoPimpleFoam, a transient compressible flow solver, we can find turbulence->divDevRhoReff(U) in it. It corresponds to the diffusion term.

We can find its definitions in different files depending on the types of the turbulence models. In the case of linear eddy viscosity models, it is defined in linearViscousStress.C file.

We can find a tiny difference by comparing it with Eq. \eqref{eq:levmdiffusion}:
l.10
\begin{equation}
\nabla \cdot \left( \mu_{eff} \left( (\nabla \overline{\boldsymbol{u}})^T -\frac{2}{3} (\nabla \cdot \overline{\boldsymbol{u}}) \boldsymbol{I} \right) \right), \tag{5} \label{eq:levmdiffusion1}
\end{equation}
l.11
\begin{equation}
\nabla \cdot \left( \mu_{eff} \nabla \overline{\boldsymbol{u}} \right). \tag{6} \label{eq:levmdiffusion2}
\end{equation}

The remaining term \(- \nabla \cdot \left( \frac{2}{3}\rho k \boldsymbol{I} \right)\) is included in the pressure gradient term.

In the next post, we’ll look into non-linear eddy viscosity models and Reynolds-stress transport models.

Thank you for taking the time to read all of my post!

Reynolds-Averaged Navier-Stokes (RANS)

Last Updated: May 11, 2019

Keywords
Boussinesq approximation, closure problem, Reynolds averaging

Reynolds Average

It is computationally expensive to resolve the wide range of time and length scales observed in turbulent flows. We now consider decomposing a flow property \(f\), such as velocity and pressure, into a mean component \(\overline{f}\) and a fluctuating component \(f’\).
\begin{equation}
f(\boldsymbol{x}, t) = \overline{f}(\boldsymbol{x}, t) + f'(\boldsymbol{x}, t), \tag{1} \label{eq:decomposition}
\end{equation}
where \(\boldsymbol{x}\) is the position vector and \(t\) is time.

The Reynolds-averaged Navier-Stokes (RANS) turbulence models aim to solve the mean flow \(\overline{f}\) that changes more slowly in time and space than the original variable \(f\). The governing equations of the mean component will be derived later.

There are many averaging operations defined in mathematics but the RANS models use the Reynolds average. It is briefly described in the newly published textbook by Kajishima and Taira [1].

For the discussion in this chapter, let us redefine the averaging operation such that it satisfies
\begin{equation}
\overline{f’} = 0,\;\;\overline{f’ \overline{f}} = 0,\;\;\overline{\overline{f}} = \overline{f}. \tag{7.2} \label{eq:reave}
\end{equation}
These relations in Eq. \eqref{eq:reave} are referred to as the Reynolds-averaging laws. The ensemble average that satisfies these laws is called the Reynolds average. This conceptual averaging operation conveniently removes fluctuating components from the flow field variables without explicitly defining the spatial length scale used in the averaging operation.

The ensemble average that appears in the above definition is defined as (and usually denoted as \(\langle f \rangle\))
\begin{equation}
\langle f \rangle(\boldsymbol{x}, t) \equiv \lim_{N \to \infty}\frac{1}{N}\sum_{i=1}^{N}f_{i}(\boldsymbol{x}, t), \tag{2} \label{eq:ensembleAve}
\end{equation}
where \(f_i\) are the samples of \(f\) and \(N\) is the number of samples. In other words, it is the average of the instantaneous values of the property at a given point in space \(\boldsymbol{x}\) and time \(t\) over a large number of repeated identical experiments. In general, this ensemble average varies with space and time (time-dependent).

For the stationary random processes, we can define the time average \(f_T\):
\begin{equation}
f_{T}(\boldsymbol{x}) \equiv \frac{1}{T} \int_{0}^{T} f(\boldsymbol{x}, t) dt, \tag{3} \label{eq:timeAve}
\end{equation}
where \(T\) is the integration time. In the case of stationary random processes, the time averages equal the ensemble averages as stated in [3]:

if the signal is stationary, the time average defined by equation \eqref{eq:timeAve} is an unbiased estimator of the true average \(\langle f \rangle\). Moreover, the estimator converges to \(\langle f \rangle\) as the time becomes infinite; i.e., for stationary random processes
\begin{equation}
\langle f \rangle(\boldsymbol{x}) = \lim_{T \to \infty} \frac{1}{T} \int_{0}^{T} f(\boldsymbol{x}, t) dt, \tag{8.28} \label{eq:aveRelation}
\end{equation}
Thus the time and ensemble averages are equivalent in the limit as \(T \to \infty\), but only for a stationary random process.

Interested readers might want to search by the keyword ”ergodic hypothesis” on the relation between the ensemble and time averages.

RANS Equations

To Be Updated

Closure Problem – Reynolds Stress

The linear eddy viscosity models (LEVM) assume the linear stress-strain relationship and employ the eddy-viscosity concept (Boussinesq approximation) introduced by Joseph Valentin Boussinesq
\begin{equation}
-\rho\overline{u_i u_j} = \mu_t \left(\frac{\partial \overline{U}_i}{\partial x_j} + \frac{\partial \overline{U}_j}{\partial x_i} \right) -\frac{2}{3}\delta_{ij}\rho k. \tag{4} \label{eq:BoussinesqApprox}
\end{equation}

rans

RANS Models in OpenFOAM

Linear Eddy Viscosity Model (LEVM)

Nonlinear Eddy Viscosity Model (NLEVM)

Reynolds Stress Model (RSM)

Limitations of LEVM
Transition Models
Differential Reynolds Stress model
  • SSG/LRR-\(\omega\)
  • JH-\(\omega^h\)
References

[1] T. Kajishima and K. Taira, Computational Fluid Dynamics: Incompressible Turbulent Flows. Springer, 2016.
[2] H. K. Versteeg and W. Malalasekera, An introduction to Computational Fluid Dynamics: The Finite Volume Method. Person Prentice Hall, 1995.
[3] W. K. George, Lectures in Turbulence for the 21st Century.