Month: January 2017

Thermal Boundary Conditions in OpenFOAM


Many thermal boundary conditions are available in OpenFOAM.
I will upload some basic cases that explain the usage of these boundary conditions.

Source Code
src/TurbulenceModels/compressible/turbulentFluidThermoModels/derivedFvPatchFields/

  • convectiveHeatTransfer

    It calculates the heat transfer coefficients from the following empirical correlations for forced convection heat transfer:
    \begin{eqnarray}
    \left\{
    \begin{array}{l}
    Nu = 0.664 Re^{\frac{1}{2}} Pr^{\frac{1}{3}} \left( Re \lt 5 \times 10^5 \right) \\
    Nu = 0.037 Re^{\frac{4}{5}} Pr^{\frac{1}{3}} \left( Re \ge 5 \times 10^5 \right) \tag{1} \label{eq:NuPlate}
    \end{array}
    \right.
    \end{eqnarray}
    where \(Nu\) is the Nusselt number, \(Re\) is the Reynolds number and \(Pr\) is the Prandtl number.

  • externalCoupledTemperature
  • externalWallHeatFluxTemperature

    This boundary condition can operate in the following two modes:
    Mode#1 Specify the heat flux \(q\)
    \begin{equation}
    -k \frac{T_p – T_b}{\vert \boldsymbol{d} \vert} = q + q_r \tag{2} \label{eq:fixedHeatFlux}
    \end{equation}
    * \(k\): thermal conductivity
    * \(q_r\): radiative heat flux
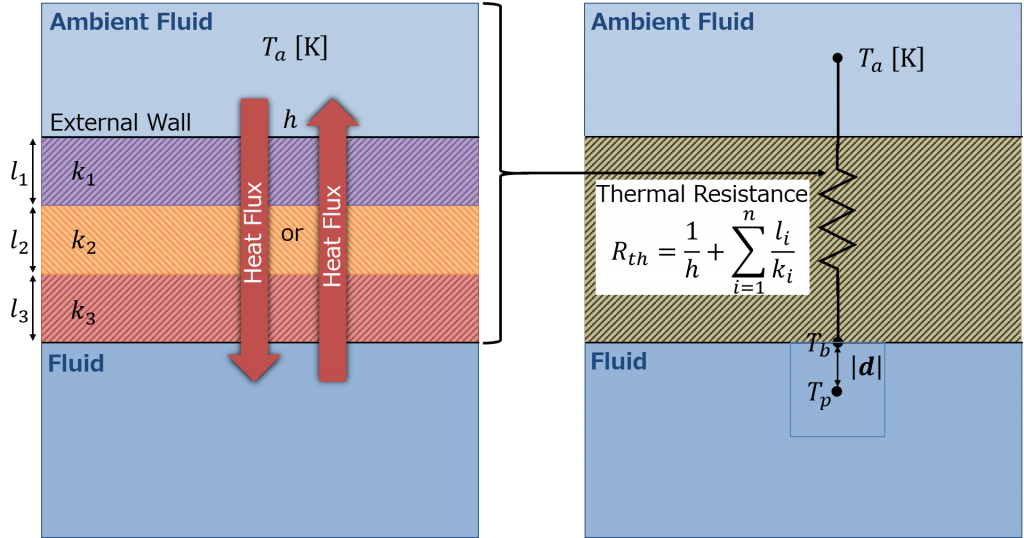
    * \(T_b\): temperature on the boundary

    Mode#2 Specify the heat transfer coefficient \(h\) and the ambient temperature \(T_a\) (Fig. 1)
    \begin{equation}
    -k \frac{T_p – T_b}{\vert \boldsymbol{d} \vert} = \frac{T_a – T_b}{R_{th}} + q_r \tag{3} \label{eq:fixedHeatTransferCoeff}
    \end{equation}
    * \(R_{th}\): total thermal resistance of convective and conductive heat transfer
    \begin{equation}
    R_{th} = \frac{1}{h} + \sum_{i=1}^{n} \frac{l_i}{k_i} \tag{4} \label{eq:Rth}
    \end{equation}

    Figure 1
  • fixedIncidentRadiation
  • lumpedMassWallTemperature

    There is a dimensionless quantity called the Biot number, which is defined as
    \begin{equation}
    Bi = \frac{l/k}{1/h} = \frac{hl}{k}, \tag{5} \label{eq:Biot}
    \end{equation}
    where \(h\) is the heat transfer coefficient, \(k\) is the thermal conductivity of a solid and \(l\) is the characteristic length of the solid. As the definition in Eq. \eqref{eq:Biot} indicates, it represents the ratio of the internal conduction resistance \(l/k\) and the external convection resistance \(1/h\). If the Biot number is small (\(Bi \ll 1\)), the solid may be treated as a simple lumped mass system of an uniform temperature. This boundary condition calculates the uniform temperature variation \(\Delta T\) on the boundary from the following equation:
    \begin{equation}
    m c_p \Delta T = Q \Delta t. \tag{6} \label{eq:lumpedmass}
    \end{equation}
    * \(m\): total mass [kg]
    * \(c_p\): specific heat capacity [J/(kg.K)]
    * \(Q\): net heat flux on the boundary [W]
    * \(\Delta t\): time step [s]

  • outletMappedUniformInletHeatAddition
  • totalFlowRateAdvectiveDiffusive
  • wallHeatTransfer
  • compressible::thermalBaffle1D
  • compressible::turbulentHeatFluxTemperature
  • compressible::turbulentTemperatureCoupledBaffleMixed
  • compressible::turbulentTemperatureRadCoupledMixed
  • compressible::alphatJayatillekeWallFunction
  • compressible::alphatPhaseChangeWallFunction
  • compressible::alphatWallFunction

Filter Width – maxDeltaxyz


Several options are available in OpenFOAM for calculation of the filter width used in the large eddy simulation (LES) and detached eddy simulation (DES). In this blog post, the maxDeltaxyz option is covered in some detail.

OpenFOAM Version: OpenFOAM-dev, OpenFOAM v1612+

Implementation in OpenFOAM

The maxDeltaxyz option calculates the filter width of the \(i-\)th cell \(\Delta_i\) by taking the maximum distance between the cell center \(P_i\) and each face center \(F_j\)
\begin{equation}
\Delta_i = {\rm deltaCoeff} \times \max_{1 \le j \le n_i} \left\{ \overline{P_iF_j} \right\}, \tag{1} \label{eq:deltaxyz}
\end{equation}
where \({\rm deltaCoeff}\) is a constant of proportion (user input) and \(n_i\) is the number of the faces of the \(i-\)th cell.

Fig. 1 Graphical illustration for the case of a regular hex cell.

For a regular hexahedral cell shown in Fig. 1, the computed \(\Delta\) using Eq. \eqref{eq:deltaxyz} equals one-half of the maximum cell width \(\Delta x\), so the deltaCoeff coefficient should be set to 2 in the turbulenceProperties file as shown below.

The filter width is calculated in the following function.

Implementation in OpenFOAM v1612+

In OpenFOAM v1612+, the face normal vectors are considered in order to take into account the mesh non-orthogonality.

Some comments

This definition \eqref{eq:deltaxyz} is often used in the detached eddy simulation (DES) where some anisotropic grid cells such as “book”, “pencil” and “ribbon”-shaped cells exist in a boundary layer mesh. The position where switching between the RANS and LES modes occurs in the DES97 model [1] depends on how to calculate the filter width \(\Delta\)
\begin{equation}
\tilde{d} \equiv {\rm min}\left( d, C_{DES}\Delta \right), \tag{2} \label{eq:dTilda}
\end{equation}
where \(d\) is the distance to the closest wall and \(C_{DES}\) is a calibration constant.
Several modified length scales have been developed to prevent a delay of the Kelvin-Helmholtz instability in free and separated shear layers [2].

References

[1] P. R. Spalart, W.-H. Jou, M. Strelets and S. R. Allmaras, Comments on the feasibility of LES for wings, and on a hybrid RANS/LES approach. 1st AFOSR Int. Conf. on DNS/LES, Aug. 4-8, 1997, Ruston, LA. In “Advances in DNS/LES”, C. Liu and Z. Liu Eds., Greyden Press, Columbus, OH.
[2] P. R. Spalart, Detached-Eddy Simulation. Annu. Rev. Fluid Mech. 41, 181-202, 2009.