Tag: renumberMesh

When we discretize the partial differential equations using the Finite Volume Method (FVM), we get sets of linear algebraic equations with large sparse coefficient matrices that are solved using iterative or direct methods. There is renumberMesh utility in OpenFOAM that is used to reduce the bandwidth of the coefficient matrices by renumbering the cell label list.

The bandwidth is not a special term in OpenFOAM but it is a general concept in the field of solving linear systems of equations. In this blog post, I will try to give a description of it and other important terms such as profile and frontwidth.

Keywords: bandwidth, profile, frontwidth, renumberMesh

Definitions of bandwidth, profile and frontwidth

The definitions of these terms are clearly described in [1]. Let \(A\) be an \(N\) by \(N\) matrix with symmetric zero-nonzero structure, i.e. , \(a_{ij} \neq 0\) if and only if \(a_{ji} \neq 0\).

The \(i\)-th bandwidth of \(A\) is:

\begin{align}
\beta_i(A) = i \; – \; {\rm min}\{ j \; | \; a_{ij} \neq 0\}. \tag{1} \label{eq:ithBandwidth}
\end{align}

The bandwidth of \(A\) is defined by

\begin{align}
\beta = \beta(A) &= {\rm max} \{ \beta_i(A) \; | \; 1 \leq i \leq N\} \\
&= {\rm max} \{ |i-j| \; | \; a_{ij} \neq 0 \}. \tag{2} \label{eq:Bandwidth}
\end{align}

The quantity \(|Env(A)|\) is called the profile or the envelope size of \(A\), and is defined by:

\begin{align}
|Env(A)| = \sum_{i=1}^{N} \beta_i(A). \tag{4} \label{eq:Profile}
\end{align}

Another quantity called frontwidth is defined by the number of rows of the envelope of \(A\) which intersect column \(i\).

\begin{align}
\omega_i(A) = \{ k \; | \; k > i \; and \; \exists l \leq i \; s.t. \; a_{kl} \neq 0 \} \tag{5} \label{eq:frontwidth}
\end{align}

To estimate factorization time, a quantity called root mean square frontwidth is introduced by [2]. This quantity is given by:

\begin{align}
f = \sqrt{\frac{1}{N} \left( \sum_{i=1}^{N} \omega_i^2 \right)}. \tag{8} \label{eq:rmsFrontwidth}
\end{align}

Output of renumberMesh utility

When the renumberMesh utility is executed, the following data is reported to the screen.

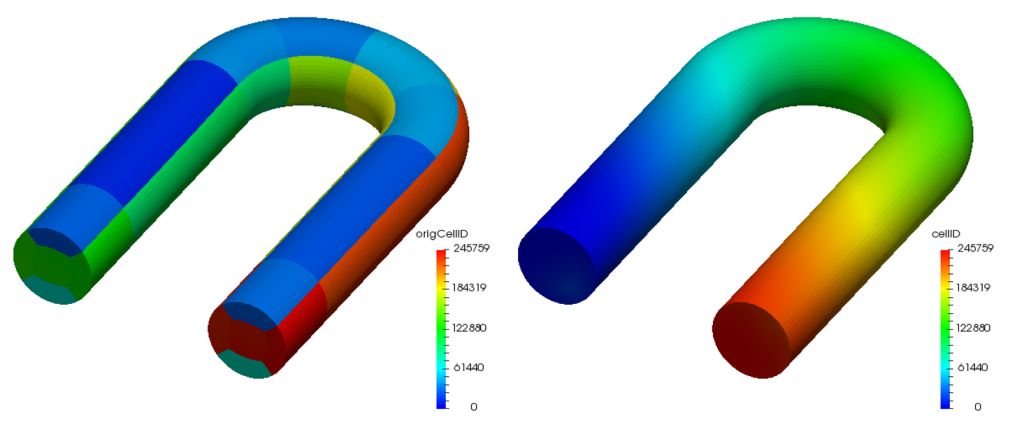
Here, the band, profile and rms frontwidth correspond to \eqref{eq:Bandwidth}, \eqref{eq:Profile} and \eqref{eq:rmsFrontwidth}, respectively. We can confirm that they all decreased after renumbering the cell label using the Cuthill-McKee (CM) algorithm. The distributions of cell labels are visually compared between before and after reordering operations in Figure 1.

Source code of renumberMesh utility

The getBand function is called from the main function. The variables band, profile and rmsFrontwidth represent \eqref{eq:Bandwidth}, \eqref{eq:Profile} and \eqref{eq:rmsFrontwidth}, respectively.

References

• [1] A NEW FAST METHOD OF PROFILE AND WAVEFRONT REDUCTION FOR CYLINDRICAL STRUCTURES IN FINITE ELEMENTS METHOD ANALYSIS (accessed 2016-05-29)
• [2] A FORTRAN PROGRAM FOR PROFILE AND WAVEFRONT REDUCTION (accessed 2016-05-29)