When we discretize the partial differential equations using the Finite Volume Method (FVM), we get sets of linear algebraic equations with large sparse coefficient matrices that are solved using iterative or direct methods. There is renumberMesh utility in OpenFOAM that is used to reduce the bandwidth of the coefficient matrices by renumbering the cell label list.
The bandwidth is not a special term in OpenFOAM but it is a general concept in the field of solving linear systems of equations. In this blog post, I will try to give a description of it and other important terms such as profile and frontwidth.
Keywords: bandwidth, profile, frontwidth, renumberMesh
| Definitions of bandwidth, profile and frontwidth |
The definitions of these terms are clearly described in [1]. Let \(A\) be an \(N\) by \(N\) matrix with symmetric zero-nonzero structure, i.e. , \(a_{ij} \neq 0\) if and only if \(a_{ji} \neq 0\).
The \(i\)-th bandwidth of \(A\) is:
\begin{align}
\beta_i(A) = i \; – \; {\rm min}\{ j \; | \; a_{ij} \neq 0\}. \tag{1} \label{eq:ithBandwidth}
\end{align}The bandwidth of \(A\) is defined by
\begin{align}
\beta = \beta(A) &= {\rm max} \{ \beta_i(A) \; | \; 1 \leq i \leq N\} \\
&= {\rm max} \{ |i-j| \; | \; a_{ij} \neq 0 \}. \tag{2} \label{eq:Bandwidth}
\end{align}The quantity \(|Env(A)|\) is called the profile or the envelope size of \(A\), and is defined by:
\begin{align}
|Env(A)| = \sum_{i=1}^{N} \beta_i(A). \tag{4} \label{eq:Profile}
\end{align}Another quantity called frontwidth is defined by the number of rows of the envelope of \(A\) which intersect column \(i\).
\begin{align}
\omega_i(A) = \{ k \; | \; k > i \; and \; \exists l \leq i \; s.t. \; a_{kl} \neq 0 \} \tag{5} \label{eq:frontwidth}
\end{align}To estimate factorization time, a quantity called root mean square frontwidth is introduced by [2]. This quantity is given by:
\begin{align}
f = \sqrt{\frac{1}{N} \left( \sum_{i=1}^{N} \omega_i^2 \right)}. \tag{8} \label{eq:rmsFrontwidth}
\end{align}
| Output of renumberMesh utility |
When the renumberMesh utility is executed, the following data is reported to the screen.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
Create time Create mesh for time = 0 Mesh size: 245760 Before renumbering : band : 217487 profile : 2793999079 rms frontwidth : 12694.49013 Renumber according to renumberMeshDict Writing renumber maps (new to old) to polyMesh. Selecting renumberMethod CuthillMcKee After renumbering : band : 978 profile : 226514746 rms frontwidth : 932.0721888 Writing mesh to "1" Written current cellID and origCellID as volScalarField for use in postprocessing. End |
Here, the band, profile and rms frontwidth correspond to \eqref{eq:Bandwidth}, \eqref{eq:Profile} and \eqref{eq:rmsFrontwidth}, respectively. We can confirm that they all decreased after renumbering the cell label using the Cuthill-McKee (CM) algorithm. The distributions of cell labels are visually compared between before and after reordering operations in Figure 1.
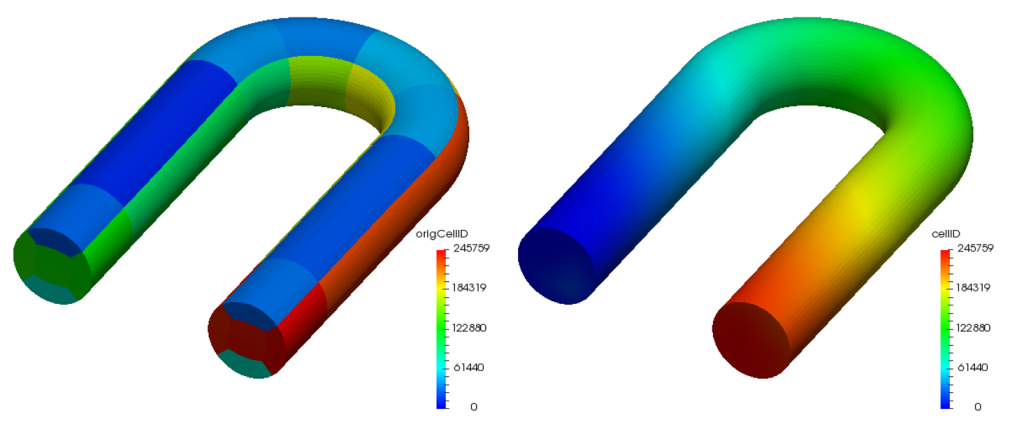
| Source code of renumberMesh utility |
|
116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 |
// Calculate band of matrix void getBand ( const bool calculateIntersect, const label nCells, const labelList& owner, const labelList& neighbour, label& bandwidth, scalar& profile, // scalar to avoid overflow scalar& sumSqrIntersect // scalar to avoid overflow ) { labelList cellBandwidth(nCells, 0); scalarField nIntersect(nCells, 0.0); forAll(neighbour, facei) { label own = owner[facei]; label nei = neighbour[facei]; // Note: mag not necessary for correct (upper-triangular) ordering. label diff = nei-own; cellBandwidth[nei] = max(cellBandwidth[nei], diff); } bandwidth = max(cellBandwidth); // Do not use field algebra because of conversion label to scalar profile = 0.0; forAll(cellBandwidth, celli) { profile += 1.0*cellBandwidth[celli]; } sumSqrIntersect = 0.0; if (calculateIntersect) { forAll(nIntersect, celli) { for (label colI = celli-cellBandwidth[celli]; colI <= celli; colI++) { nIntersect[colI] += 1.0; } } sumSqrIntersect = sum(Foam::sqr(nIntersect)); } } |
The getBand function is called from the main function. The variables band, profile and rmsFrontwidth represent \eqref{eq:Bandwidth}, \eqref{eq:Profile} and \eqref{eq:rmsFrontwidth}, respectively.
|
651 652 653 654 655 656 657 658 659 660 661 662 663 664 665 666 667 668 669 670 671 672 673 674 675 676 677 678 679 680 681 682 683 684 685 686 687 688 |
const bool readDict = args.optionFound("dict"); const bool doFrontWidth = args.optionFound("frontWidth"); const bool overwrite = args.optionFound("overwrite"); label band; scalar profile; scalar sumSqrIntersect; getBand ( doFrontWidth, mesh.nCells(), mesh.faceOwner(), mesh.faceNeighbour(), band, profile, sumSqrIntersect ); reduce(band, maxOp<label>()); reduce(profile, sumOp<scalar>()); scalar rmsFrontwidth = Foam::sqrt ( returnReduce ( sumSqrIntersect, sumOp<scalar>() )/mesh.globalData().nTotalCells() ); Info<< "Mesh size: " << mesh.globalData().nTotalCells() << nl << "Before renumbering :" << nl << " band : " << band << nl << " profile : " << profile << nl; if (doFrontWidth) { Info<< " rms frontwidth : " << rmsFrontwidth << nl; } |
| References |
- [1] A NEW FAST METHOD OF PROFILE AND WAVEFRONT REDUCTION FOR CYLINDRICAL STRUCTURES IN FINITE ELEMENTS METHOD ANALYSIS (accessed 2016-05-29)
- [2] A FORTRAN PROGRAM FOR PROFILE AND WAVEFRONT REDUCTION (accessed 2016-05-29)
Hi fumiya
How did you make the cell ID plot in Paraview? I’m trying to do the same, but I can’t quite figure it out
Just use foamToVTK command, and use CellID in paraview.
Regards,
Vahid
It’s a nice expalanation! Thank you!